Approximation of irrational numbers

Let α be an irrational number. Its decimal representation is then nonterminating and nonrepeating. One can write

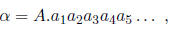
where A is the integral part of α. For instance,

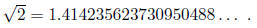
To approximate sqrt(2), we may take its truncated decimal expansions as follows:

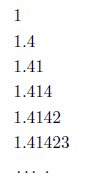
All numbers in the preceding p sequence are rational and they converge to
sqrt(2) from below. In fact, the difference between sqrt(2)and its n-th rational
approximation is smaller than 10^1-n. To achieve a good approximation,
one needs to choose n sufficiently large:

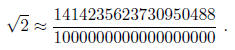
Could a good approximation of sqrt(2) have a not so large denominator?
Indeed, if possible, we would like to operate with smaller integers. Take a
look at the following example.

EXAMPLE. Among all rational fractions with denominator 12, the one
closest to sqrt(2) is 17/12,

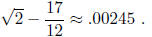
At the same time,

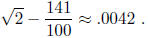
Obviously, 17/12 is a better approximation than 1.41, and its denominator
is about 8 times smaller

Let’s introduce a measure of our approximation of α by a rational number
p/q, the approximation coefficient:

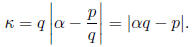
If 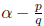is small and q is not so large, then the coefficient is small.
Conversely, if is small, then 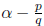is even smaller. Thus the size of k tells
us about the quality of our approximation.

EXAMPLE. Out of three approximations, 3/2, 7/5, and 1.41, to sqrt(2), which
one has the smallest k? A quick computation gives the answer:

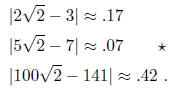
Given the size of its denominator, 7/5 is a very good choice. But 17/12 is,
of course, better than all three.

How to find these good approximations? Do they always exist? The true
answer has to do with continued fractions. We’ll only look at a partial
explanation here.

THEOREM. Let α be a given irrational number, and let N be any positive
integer. Then there exists a rational fraction p/q such that

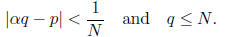
In particular,

The preceding fact has an interesting illustration. Consider the family of
horizontal lines y = q, where q = 0, 1, 2, 3, . . . , and the family of parallel
lines x = αy − p, where p = 0,±1,±2,±3, . . . . The two families intersect
in a lattice of points with components (αq − p, q). For instance, the line
y = 3 meets the line x = αy − 5 at (3α − 5, 3).

Thus to each rational fraction p/q we put in correspondence a point
(αq − p, q), whose x-component has absolute value k and whose
y-component is the denominator q. Now draw a rectangle with vertices

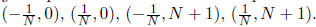The theorem says that for any
choice of N, the rectangle must contain a lattice point in its interior. Even
if N is very very large, i.e. the rectangle is very very thin.

Plot and experiment to get a better understanding. If you carefully
examine this geometric construction, you may see a way to prove the
theorem.