- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Building and Teaching a Math Enhancement
| INTRODUCTION |
Team Members:
George Fetch : Industrial Arts and Drivers Ed. @ Benton Area School District
Jeremy Chapin: Special Ed. Math and English @ Benton Area School District
Title of the Lesson: Making a Trivet
PA Math Standard(s) Addressed by the Lesson:
2.3.8 A – Develop formulas and procedures for determining measurements
(e.g. area,
volume, distance)
2.3.8 D – Estimate, use and describe measures of distance, rate,
perimeter, area, volume,
weight, mass, and angles.
Assessment Anchor Codes:
M8.B.2 - Apply appropriate techniques, tools, and formulas to determine
measurements
| BUILDING A MATH ENHANCEMENT |
1. Objective of the lesson.
Students will demonstrate a working knowledge of
Adding and dividing fractions (math concept) and its application in Wood
Working (technical field), while recognizing it in other contexts.
2. Identify the math, math terms and vocabulary and write out the description
or
definitions.
a. Planing- A process by which a board is smoothed and dimensioned to
adjust the
thickness by use of a planing machine.
b. Denominator- The bottom number in a fraction.
c. Numerator- The top number in a fraction.
d. Reciprocal- a fraction written upside down.
e. Cross-cut- Cutting a board across the grain.
f. Rip-cut- Cutting a board with the grain.
g. Jointing- Planing the edge of a board.
• Fraction addition – (remember to use a common denominator)
• Fraction Subtraction- (remember to use a common denominator)
• Fraction Division- (remember to use the reciprocal)
3. Note the steps, rules, underlying principles of the concept or theory and
summarize.
The following steps must be followed in sequential order:
1. Plane the board
2. Joint edges of board
3. Cross cut board
4. Rip cut board
5. Notch the board
6. Sand and assemble board
4. Develop 8-10 sample problems, moving from very specific wood working
technology examples to more generic problems.
1. Given a 1 inch thick board, how many times would it have to be run through a
planer that planes 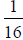 of an inch per cut to make
the board
of an inch per cut to make
the board 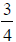 of an inch thick?
of an inch thick?
2. Given a 1 inch thick board, how many times would it have to be run through a
planer that planes 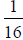 of an inch per cut to make
the board
of an inch per cut to make
the board 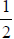 of an inch thick?
of an inch thick?
3. With 15 students in a class, is a board that is 8 ft. in length, long enough
for each
student to have a 6 in. long piece?
4. How long would a board have to be to make a trivet with each section being 2
inches long.
5. If a 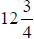 board is cut into three equal pieces,
what would be the length of each
board is cut into three equal pieces,
what would be the length of each
piece?
6. Pick any 5 boards from the lumber pile and measure them to the nearest
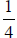 inch.
inch.
7. What is half of 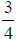 ?
?
8. What is 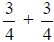 ?
?
9. What is 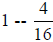 ?
?
5. Document references and supplies needed to
demonstrate the math concept.
FUNDAMENTALS OF MATH with Career Applications. Copyright 2002 Pearson
Education Inc.
Curriculum based practice problems directly from lesson
Dry-Erase board
Various boards from lumber pile for the students to measure
6. Describe lesson adaptations for students with special needs.
- Give students written directions and frequently repeat oral directions
- Work with a partner
- Break assignments into smaller steps
7. Provide sample handouts for students and presentation materials for
teachers,
as appropriate.
| TEACHING A MATH ENHANCEMENT |
Title of the Lesson: Making a Trivet
1. Introduction to the lesson.
I am going to introduce the lesson by showing them a finished trivet and briefly
telling them how we are going to go about making one from a rough piece of
lumber.
2. Assess students’ math awareness by asking questions.
How do you add fractions with uncommon denominators?
How do you subtract fractions with uncommon denominators?
How do you divide fractions with uncommon denominators?
How do you convert feet to inches?
3. Demonstrate the example problem that is embedded in the Wood-working
technology curriculum.
Question
- Given a 1 inch thick board, how many times would it have to be run through a
planer that planes ![]() of
an inch per cut to make the board
of
an inch per cut to make the board
![]() of an inch thick?
of an inch thick?
Solution
- Step #1 – Find a common denominator for our fractions, which would be
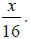
- Step #2 – Determine how many 16ths are in 1 inch and in
![]() of an inch.
of an inch.
- Step #3 – Set up the equation as follows and solve:
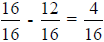
- Step #4 – After determining the difference between 1 inch and
![]() of an
of an
inch in 16ths is 4, we can know we have to run it through the planer 4
times.
4. Explain the math concept or theory and show students how it applies, using
the
terminology of math.
*Adding Fractions (ex. 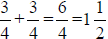 )→When adding
fractions, add the
)→When adding
fractions, add the
numerators together while keeping the denominators the same; reduce when
necessary.
*Subtracting fractions (ex.
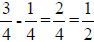 )→When subtracting fractions, subtract the
)→When subtracting fractions, subtract the
numerators while keeping the denominators the same; reduce when necessary.
*Dividing fractions (ex.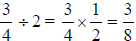 )→When dividing
fractions we use the
)→When dividing
fractions we use the
reciprocal of the divisor and simply multiply the numerators and the
denominators.
5. Demonstrate other examples as necessary.
a. If a ![]() board is cut
into three equal pieces, what would be the length of each
board is cut
into three equal pieces, what would be the length of each
piece?
b. Pick any 5 boards from the lumber pile and measure them to the nearest
![]() inch.
inch.
c. What is half of ![]() ?
?
d. What is 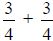 ?
?
6. Have students explain the solutions to the problems, or demonstrate what
they
did to show understanding. Correct answers are in ( ).
A. Given a 1 inch thick board, how many times would it have to be run
through a planer that planes
![]() of an inch per cut to
make the board
of an inch per cut to
make the board ![]() of
of
an inch thick? (4 times)
B. Given a 1 inch thick board, how many times would it have to be run
through a planer that planes
![]() of an inch per cut to
make the board
of an inch per cut to
make the board ![]() of
of
an inch thick? (8)
C. With 15 students in a class, is a board that is 8 ft. in length, long enough
for each student to have a 6 in. long piece?
(8ft.=96in. 6in.x15students=90 –Yes)
D. How long would a board have to be to make a trivet with each section
being 2 inches long? (6in.)
E. If a
![]() in. board is cut into
three equal pieces, what would be the length
in. board is cut into
three equal pieces, what would be the length
of each piece? ( 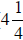 in.)
in.)
F. Pick any 5 boards from the lumber pile and measure them to the
nearest ![]() inch. (Answers
will vary)
inch. (Answers
will vary)
G. What is half of ![]() ?
?
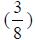
H. What is 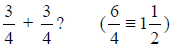
7. Challenge students to write and solve their own example problems and
demonstrate competency in a test situation.
• At this point I would have the students come up with ten of their own
problems and solutions relating to the math that we are doing in our shop
class.
e.g. I would be looking for any math problem the kids could come up on
their own that involved anything along the lines of adding, subtracting, or
dividing fractions.


