- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Functions
Equal Functions
| Two functions f and g are equal if they have the same domain D, and f(d) = g(d) for all d in D. |
Inverse Functions
| Let f be a one-to-one correspondence from the set
A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f(a) = b. The inverse function of f is denoted f -1. Thus, f -1(b) = a when f(a) = b, so f -1(f(a)) = a. |
As we observed, the function f(x) = x + 1 from the set of
integers to the set of integers is a
bijection. To reverse the correspondence, let y = f(x) = x + 1. Thus, we know
that x = y – 1.
Consequently, f -1(y) = y – 1.
Note that not all functions have an inverse. A one-to-one correspondence is
called invertible since
we can define an inverse of this function. However, a function is not
invertible
if it is not a one-to-
one correspondence, since the inverse of such a function does not exist. For
example, the
function f(x) = x2 from the set of integers to the set of integers is
not invertible since it is not one-to-
one. Since f(-1) = f(1) = 1, the inverse of f would have to assign two elements
to 1, which
violates the definition of a function. Hence, an inverse of f cannot exist in
this case.
Composition of Functions
Consider two functions: successor as applied to integers, and a sqr (“square”)
function. If we take
the output of the successor function and use it as input to the sqr function,
the two functions are
operating together. They take as input an integer n, add one to it and then
square n+1. We call this
a composition of two functions.
| Let g be a function from the set A to the set B
and let f be a function from the set D to the set C (where B is a subset of D). The composition of f and g, denoted by (f o g), is a function defined by: (f o g)(a) = f(g(a)) where a is an element of A. f o g may also be read "f circle g". |
Here is a diagram to illustrate (in this case B = D):
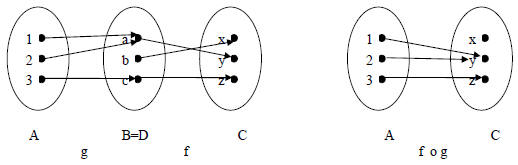
So (f o g)(1) = y, (f o g)(2) = y, and (f o g)(3) = z.
always true that g(f(a)) = f(g(a)). Indeed, for a simple
example of this, consider the case where g
has the set A as a domain and g has the set D as a domain, and the sets A and D
contain no
elements in common. Then, while f(g(a)) may be defined, g(f(a)) is undefined,
since f does not
operate on element a. In the diagram above, we cannot form g o f, because the
co-domain of f is
not a subset of the domain of g. f always produces a result in the set {x, y,
z}, and g does not
operate on these values.
Notice also that in the successor-sqr example, the composition is not
commutative since (n + 1)2 ≠
n2 + 1 (except for n = 0).
As an additional example, let f and g be functions from the real numbers to the
real numbers
defined as follows:
f(x) = 2x + 3
g(x) = 3x + 2
The composition of f and g is: (f o g)(x) = f(g(x)) = f(3x
+ 2) = 2(3x + 2) + 3 = 6x + 7
The composition of g and f is: (g o f)(x) = g(f(x)) = g(2x + 3) = 3(2x + 3) + 2
= 6x + 11
Thus both compositions are defined, but (f o g)(x) ≠ (g o f)(x).
A Few Important Functions
Now that we have all the definitions out of the way, there are a few functions
that appear on
occasion in computer science that are worth specifically identifying.
Identity Function
| Let I be a function from the set A to set A
defined by I(a) = a for all a in A. The function I is called the identity function. |
Floor Function
| The floor function assigns to the real
number x the largest integer that is less than or equal to x. The floor function applied to x is denoted 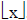 . . |
Ceiling Function
| The ceiling function assigns to the real
number x the smallest integer that is greater than or equal to x. The floor function applied to x is denoted 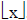 . . |
Examples:
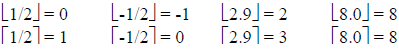
Proofs with Functions
Here are some examples of proofs with functions.
Problem: Prove: if f is a function from set A to set B that is a
one-to-one-correspondence, then the
inverse function f -1 is one-to-one and onto (i.e., it is also a
one-to-one correspondence).
Proof: First we show f -1 is onto. If a is in A, then since f
is a function, there is a b in B such that
f(a) = b. Hence, by definition of inverse function, f -1 (b) = a,
where b is in the domain of f -1 and a
is in the co-domain of f -1. Note that for any element a in A, f
-1 (b) = a must hold for some b in B
in order for f -1 to be the inverse function of f. As a result, f
-1 is onto (the set A).
Now, we show f -1 is one-to-one. Assume that some b' and b exist in B
such that f -1 (b) = f -1 (b') =
a. If this is true, then f(a) = b and f(a) = b'. But since f is a function, it
implies that b = b'
(otherwise, f would violate the definition of a function). Since b = b' in all
such cases, it follows
that f -1 (b) = f -1 (b') implies that b = b'. Thus, f
-1 is one-to-one (by the definition of one-to-one).
QED.
Problem: Let g be an invertible function from A to
B and f be an invertible function from B to C.
Prove or disprove: (f o g) -1 = g -1 o f -1.
Proof: First, note that g and f are bijections, that (f o g) is a
bijection from A to C, and thus
(f o g) -1 exists and is a bijection from C to A. (Proofs of these
facts are left to the reader.)
Consequently, by the definition of a function, for any c in C, there must be
some a in A such that
(f o g) -1(c) = a. We now use this as a basis to prove that (f o g)
-1
= g -1 o f -1
.
| 1. (f o g) -1(c) = a implies (f o g)(a) = c | Definition of inverse function applied to (f o g) |
| 2. (f o g)(a) = c implies f(g(a)) = c, meaning
that there exists b in B such that g(a) = b and f(b) = c |
Definition of composition |
| 3. g(a) = b implies g -1(b) = a and f(b) = c implies f -1(c) = b |
Definition of inverse function applied to g and f |
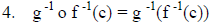 |
Definition of composition |
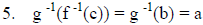 |
Substituting f -1(c) = b and g -1(b) = a from step 3 |
6. Thus,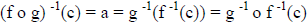 |
Combining steps 1, 4 and 5 |
Hence, we have shown that (f o g) -1(c) = g
-1 o f -1(c) for any arbitrary c in C, where C is the
domain of (f o g) -1. Thus, it follows that this equality must hold
generally for all elements of the
domain of (f o g) -1, so (f o g) -1 = g -1 o f
-1.
QED.
Problem: Prove or disprove that
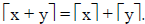
Proof: This statement is actually false. Consider the counter-example
where x = ½ and y = ½.
Here, 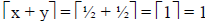 , whereas
, whereas
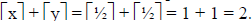
Bibliography
For additional information on functions, consult Discrete Math textbooks or
Calculus
textbooks. The following are excellent references:
S. Epp, Discrete Mathematics with Applications, Belmont, CA: Wadsworth, 1990.
R. McEliece, R. Ash, C. Ash, Introduction to Discrete Mathematics, New York:
Random
House, 1989.
K. Rosen, Discrete Mathematics and its Applications 6th Ed., New York:
McGraw-Hill, 2007.
Historical Notes
The term "function" and the form (x, f(x)) is attributed to Leibniz who used it
to refer to
several of his mathematical formulas, but the concept of a function was first
presented by René
Descartes (1596-1650) in his Geometry of 1637. In this book, he presents the
concept of
defining an equation in terms of one variable (i.e., as a function of...), and
how to graph
equations in the Cartesian plane. The formal definition of a function (as a
mapping from
domain to target) was first formulated for sets of numbers by Lejeune Dirichlet
(1805-1859) in
1837.


