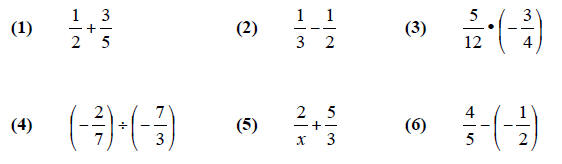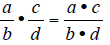Fractions

The thing that strikes me most about students and fractions is the misuse of “shortcuts”
and the procedures required for each operation. I always begin with simplifying
fractions. Because of the future algebra class, particularly rational expressions, heading
their way, I teach simplifying by factoring. It’s really difficult to simplify polynomial
numerators and denominators without factoring.

Students really need to understand prime factorization to accomplish simplification of
fractions. I hear students say that the twos will cancel out. This is actually not true.
They really divide out for one.

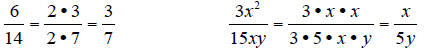
The one topic of fractions that seems to try many students is that of common
denominator. Students should be reminded of the procedures for each operation. The
only operations requiring a common denominator are adding and subtracting.
Multiplication and division do not require common denominators.

Rule: To Add Two Fractions	Rule: To Subtract Two Fractions
Rule: To Multiply Two Fractions	Rule: To Divide Two Fractions

Before practicing with negative fractions, it might be wise to check the basic fraction
understanding from the previous rules.

Combine and simplify the fractions.

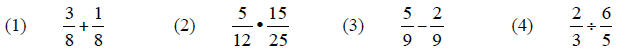
answers:

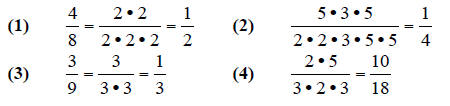
After checking for the most basic use of the rules, the idea of common denominator and
equivalent fractions must be addressed.

For equivalent fractions, I like to use a number line in the following way. I have the
students draw three number lines. I then have them label from zero to one. On the first
number line, I have them put one mark exactly between zero and one. On the second
line, I have them put the one mark in the middle and then one mark in the middle of the
two resulting segments. One the third line, they do the same, except they then bisect each
of the four segments. Then I ask them how many segments they have traveled to the
middle. We put this over the total number of segments. It becomes visually clear to
them. This exercise suggests that a fraction can look different from another, yet still have
the same numerical value on the number line.

When first working with equivalent fractions, I like to start with a particular fraction and
then ask them to write the equivalent fraction with a given denominator.

For instance, find the equivalent fraction to 2/5 that has a denominator of 20.

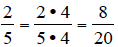
To build fractions to “higher terms,” use multiplication in the numerator and the
denominator.

Find the equivalent fraction to 20/30 that has a denominator of 15.

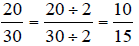
To reduce fractions to “lower terms,” use division in the numerator and the denominator.

The previous is different from reducing to “lowest terms.” Lowest terms would leave no
common factors at all between the numerator and denominator.

After introducing the idea of equivalent fractions, students are ready to find the LCD
(least common denominator). There are so many ways to do this, but I find that factoring
works best when dealing with variable factors.

To ad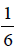d and 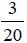we need a common denominator.

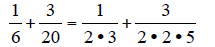
By rewriting with factored denominators, we can see missing that need to be multiplied
into the denominator and numerator of each fraction.

From above, we can see that the first denominator needs one factor of 2 and one factor of
5 to match with the second denominator. The second denominator needs one factor of 3
to match up with the first denominator.

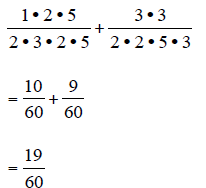
This works especially well with fractions containing variables.

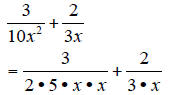
The first denominator needs one factor of 3. The second denominator needs one factor of
2, one factor of 5, and one factor of x.

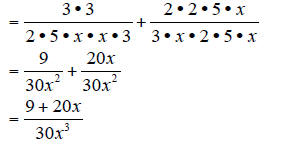
Practice Problems: