Math 35 Practice Final

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Answer the question.

1) What is the reciprocal of 2/3?

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

2) Given a nonzero fraction, how do you write its reciprocal?
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

3) In a fraction, the number that is written below the fraction bar is called the ? .
A) denominator B) quotient C) difference D) numerator

4) Show how to reduce 63/84 to lowest terms.

Perform the operation. Write the answer as a fraction in lowest terms.

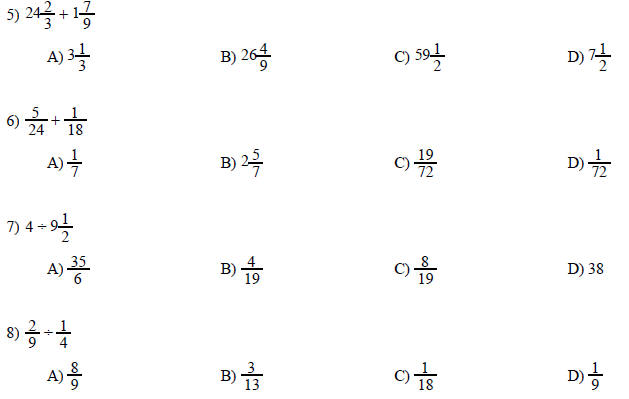
Write the number in prime factored form.

Answer the question as instructed.
15) Which of the following statements is false?

A) 18 < 18 B) 18 ≤18 C) 18 ≥ 18 D) 18 = 18

16) True or false? In an inequality using > or <, the inequality symbol should point toward the larger number
for the inequality to be true.
A) true B) false

17) Which of the following is the correct way to evaluate the expression 6 + 4 · 4?
A) 6 + 4 · 4 = 16 + 4 = 28 B) 6 + 4 · 4 = 6 + 16 = 22
C) 6 + 4 · 4 = 10 · 4 = 40 D) 6 + 4 · 4 = 24 + 16 = 40

18) Which of the following is not a mathematical sentence?
A) 3 · 3 = 9 B) 3 · 3 · 9 C) 3 < 3 D) 3 ≠ 6

Find the value of the exponential expression.

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Write the statement in words and decide whether it is true or false.

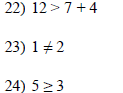
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Write the word statement in symbols.

25) Two is less than or equal to five.

25) Two is less than or equal to five.
A) 2 > 5 B) 2 < 5 C) 2 ≥ 5 D) 2 ≤ 5

26) Six is equal to eleven minus five.
A) 6 - 11 < 5 B) 11 = 6 - 5 C) 11 < 6 + 5 D) 6 = 11 - 5

Find the value of the expression.

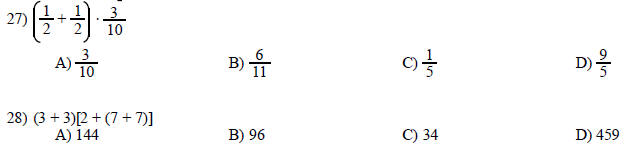
Simplify.

State the phrase as a mathematical expression. Use x to represent the variable.

32) The quotient of a number and four
A) x/4 B) 4 - x C) 4 + x D) 4x

33) Eight times a number, added to 45
A) 8x B) 8(x + 45) C) 8 · 45 + x D) 8x + 45

34) The difference between two times a number and seven
A) 2 - x + 7 B) 2x - 7 C) 7 + 2x D) 7 - 2x

35) A number increased by twelve
A) 12x B) x - 12 C) 12 D) x + 12

Decide if the given number is a solution to the given equation.

36) p + 3 = 11; 8
A) No B) Yes

Find the numerical value of the expression for a) x = 4 and b) x = 18.

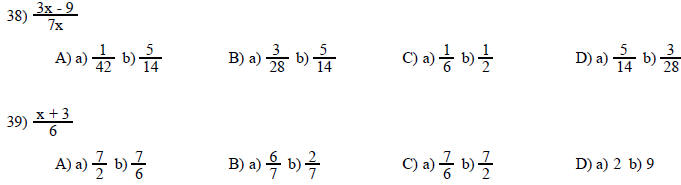
Write this word statement as an equation. Use x as the variable, and find all solutions from the set {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

40) The sum of a number and 5 is 9.
A) x = 5 + 9 ; 14 B) x + 9 = 5; 4 C) x + 5 = 9; 4 D) x + 5 = 9; 9

41) 48 divided by a number equals 1/3 times that number.

Change the word statement to an equation. Use x as the variable.

42) The product of twice a number and 3 is 30.
A) 6x = 30x B) 6x = 30 C) 2x + 3 = 30

Simplify.
43) |2 - 8|
A) -6 B) 0 C) 12 D) 6

Find the sum.

44) 20 + [23 + (-5)]
A) 48 B) 38 C) -8 D) 2

45) [4 + (-14)] + [1 + (-18)]
A) 7 B) -27 C) 37 D) -29

46) -320 + 518
A) -838 B) -198 C) 838 D) 198

47) -8 + (-17)
A) -25 B) 25 C) 9 D) -9

Find the difference.

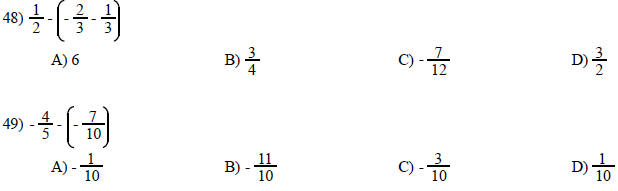
TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false.

Provide an appropriate response.
50) The product of two negative numbers is negative.

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

51) What values of a and b make the result negative? -(a - b)

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Find the quotient.

Perform the indicated operation.

Give the numerical coefficient of the term.

57) -w
A) 1 B) 0 C) -1 D) -w

58) -2y
A) y B) 2y C) 2 D) -2

Simplify the expression.

59) 6 + 5(17 - 3m)
A) 91 - 15m B) 85 - 15m C) 91 + 15m D) 91 - 3m

60) -7 - (3 - 6s)
A) 4 - 6s B) 10 + 6s C) -4 - 6s D) -10 + 6s

Solve the equation.

Solve the problem.

63) Two pages that face each other in a book have 353 as the sum of their page numbers. What is the number
of the page that comes first?
A) 174 B) 176 C) 175 D) 177

64) The difference between two positive integers is 36. One integer is three times as great as the other. Find
the integers.
A) 36 and 54 B) 18 and 36 C) 18 and 54 D) 54 and 90

Find the measure of each marked angle.

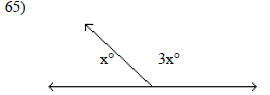
A) 45° and 135° B) 90° and 270° C) 45° and 55° D) 60° and 120°

Use a formula to solve the problem.

66) A baking pan measures 12 inches long, 5 inches wide, and 2 inches deep. What is the volume of the pan.
A) 60 cubic inches B) 19 cubic inches
C) 120 cubic inches D) 34 cubic inches

Solve the equation.

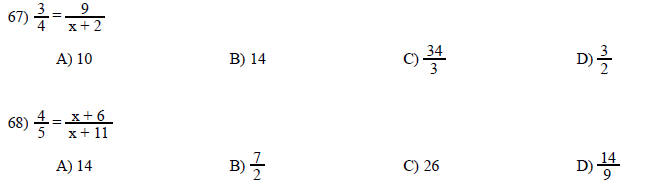
Solve the problem.
69) Janet drove 244 kilometers and the trip took 4 hours. How fast was Janet traveling?
A) 61 km/hr B) 1/61 km/hr C) 976 km/hr D) 62 km/hr

70) From a point on a straight road, John and Fred ride bicycles in opposite directions. John rides 7 miles per
hour and Fred rides 9 miles per hour. In how many hours will they be 80 miles apart?
A) 5 hours B) 6 hours
C) Not enough information D) 4 hours

71) How many liters of a 30% alcohol solution must be mixed with 80 liters of a 90% solution to get a 80%
solution?
A) 9.6 L B) 96 L C) 1.6 L D) 16 L

72) A cashier has a total of 128 bills made up of fives and tens. The total value of the money is $660. How
many ten-dollar bills does the cashier have?
A) 4 ten-dollar bills B) 124 ten-dollar bills
C) 2 ten-dollar bills D) 6 ten-dollar bills

Write an inequality involving the variable x that describes the set of numbers graphed.

Complete the ordered pair for the given equation.

Complete the table of values for the given equation.

Decide whether or not the ordered pair is a solution to the equation.
77) 14x - 7y = -56; (-5, -2)
A) No B) Yes

Find the intercepts for the graph of the equation.

78) -2x - 4y = 0
A) (-0, -8) (-4, 0) B) (-4, 0) (-8, 0) C) (0, -4) (0, -8) D) (0, 0) (0, 0)

79) 3x + y = 3
A) (1, 0) (0, 3) B) (3, 6) (-1, 3) C) (0, -1) (0, 6) D) (-1, 0) (6, 0)

Graph the linear equation.

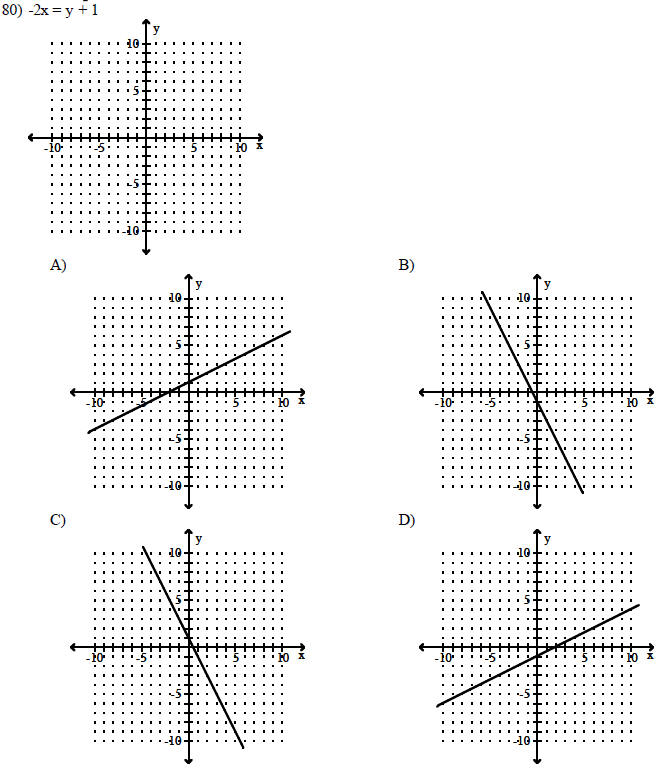
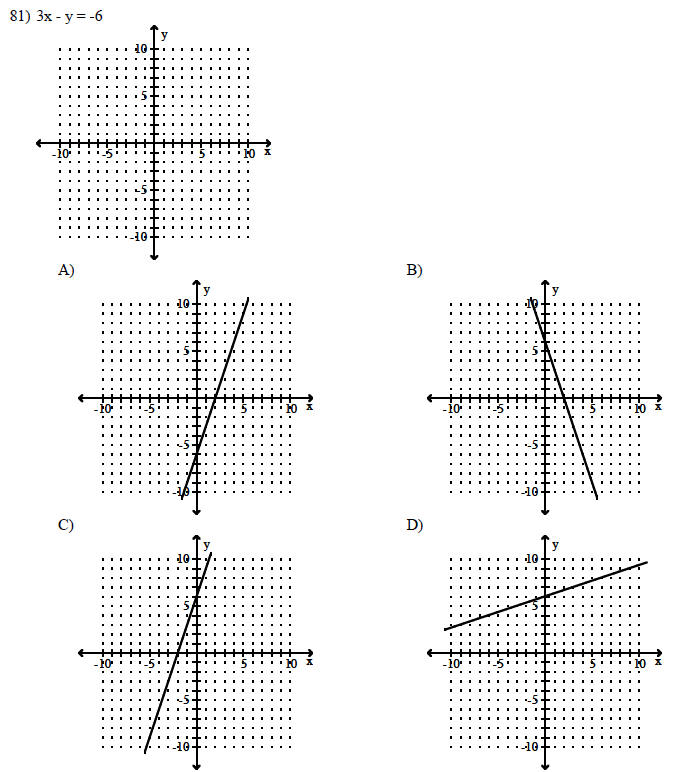
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Provide the proper response.
82) Give a definition of the slope of a vertical line.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Find the slope of the line.

Find the slope of the line going through the given pair of points.

Determine whether the graphs of the equations are parallel lines, perpendicular lines, or neither.

85) 6x + 2y = 8
12x + 4y = 17
A) Parallel B) Neither C) Perpendicular

Solve the problem.

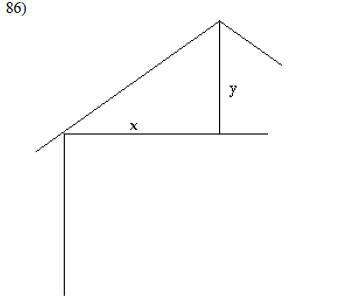
Let x = 12 and y = 3. Find the pitch of the roof.

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Answer the question or write an explanation.
87) Describe a situation in which the point-slope form would be more useful than the slope-intercept
form.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question

Find an equation in slope-intercept form of the line satisfying the specified conditions.

88) Through (1, 6), parallel to -8x + 9y = 19

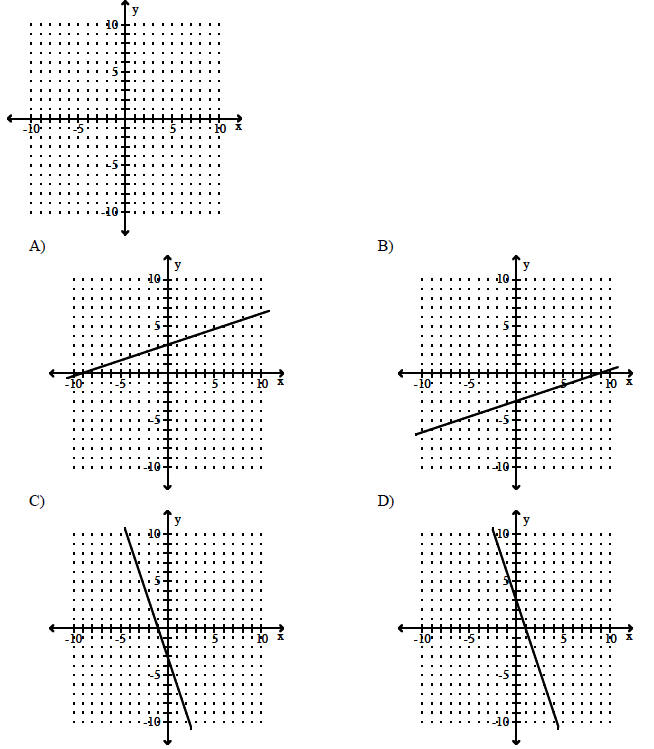
Graph the line.
89) Through (0, 3), m = - 3

Write an equation of the line through the given point with the given slope. Write the equation in slope-intercept form.

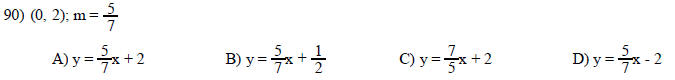
Write the slope-intercept form of the equation for the line passing through the given pair of points.

91) (9, -8) and (9, 4)
A) 4x - 8y = 0 B) y = -8 C) -8x + 4y = 0 D) x = 9

Use the geometric interpretation of slope (rise divided by run) to find the slope of the line. Then, by identifying the y-intercept from the graph, write the slope-intercept form of the equation of the line.

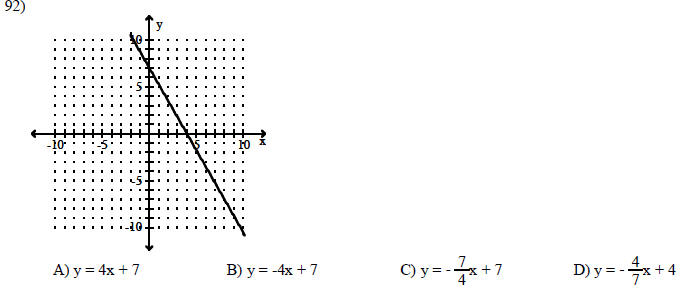
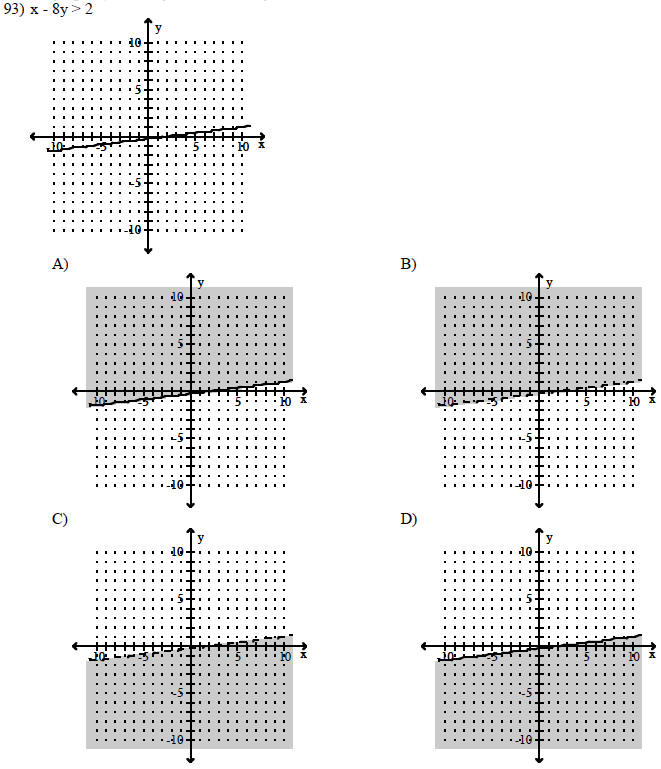
Complete the graph by shading the correct region.

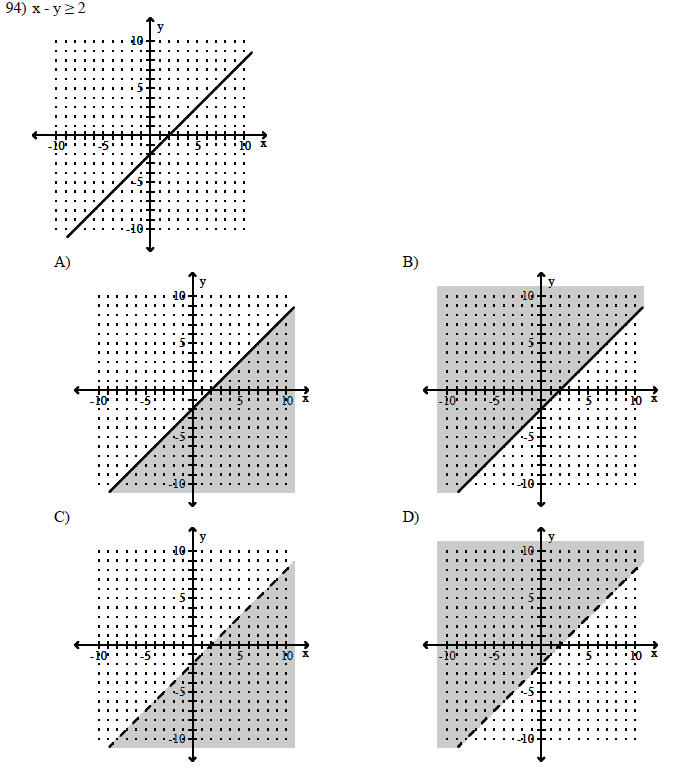
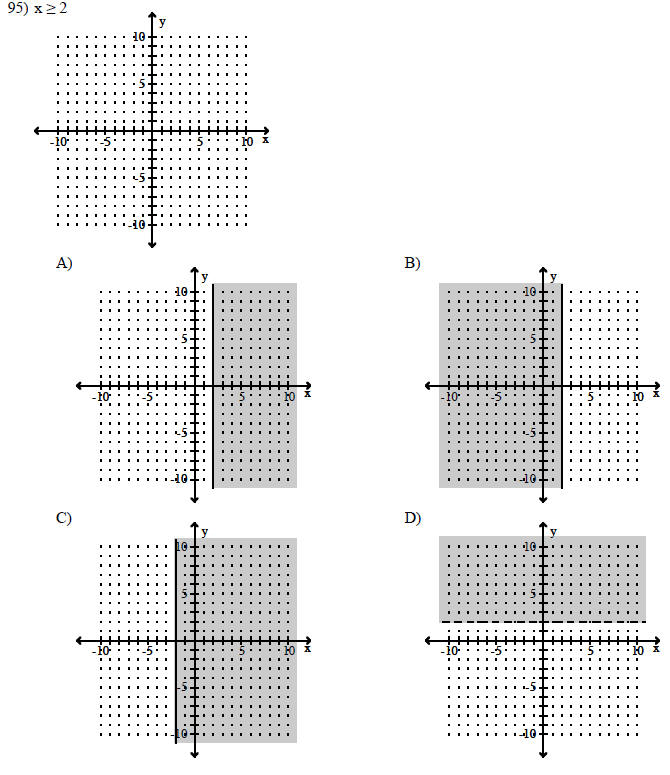
Graph the linear inequality.

Decide if the graph of the system is a pair of parallel lines, intersecting lines, or one line.

97) x + 2y = 8
2x - 4y = 0
A) Parallel B) Intersecting C) One Line

98) x + 3y = 8
2x + 6y = 16
A) Intersecting B) One Line C) Parallel

Without solving, tell if the system is inconsistent, the equations are dependent, or neither.

99) x + 4y = 20
2x + 8y = 40
A) Neither B) Inconsistent C) Dependent

100) x + y = 1
2x - 2y = 1
A) Inconsistent B) Dependent C) Neither

Decide whether or not the ordered pair is a solution of the system.

101) (5, 5)
x + y = 0
x - y = -10
A) No B) Yes

102) (5, -3)
3x + y = 12
4x + 3y = 11
A) Yes B) No

Does the system have one solution, no solution, or an infinite number of solutions?
103) x - 2y = 5
2x - 4y = 18
A) No Solution B) One C) Infinite number

104) 2x - y = 5
-4x + 2y = -18
A) One B) Infinite number C) No Solution

Solve the problem.
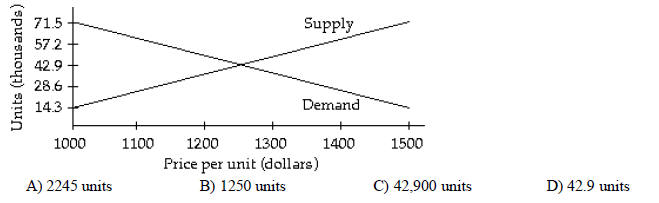
105) The graphs below represent the supply and demand for a product at various prices per unit. How many
units should be produced so that supply equals demand?

Solve the system by graphing.
106) x = -y
y + x = 6

A) B) {(1, 5)}
C) {(1, 1)} D) Infinite number of solutions

107) 2x + y = 8
4x + 2y = 16

A) {(5, -2)} B)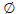
C) Infinite number of solutions D) {(0, 8)}

Find the equations of the system shown on the graphing calculator screen.

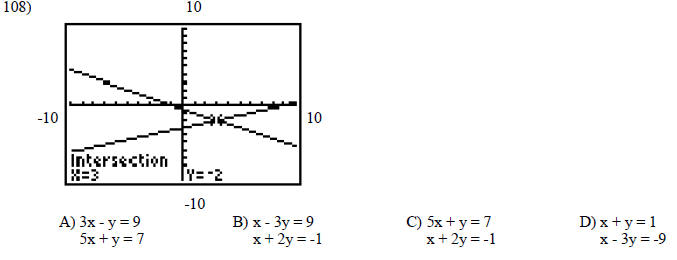
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Provide an appropriate response.
110) A student solved the system of equations
x + 2y = 4
3x + 6y = 12
for x in the first equation, and substituted into the second equation. The y's also disappeared in the
process. The student claimed that the system of equations has no solution. Is this correct?

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

111) When solving a system of equations, you get x + 2 = x - 5. How many solutions are there?
A) One solution B) No solutions C) Infinitely many

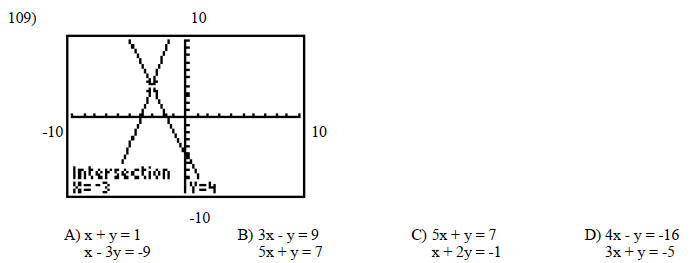
Clear fractions then solve by substitution.

Solve by the substitution method.
113) x + y = 3
x + y = -8
A) Infinite number of solutions B) {(0, -5)}
C) 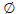D) {(3, -8)}

Solve the system by the elimination method.
114) 7x - 4y = 72
2x - 2y = 24
A) {(8, -4)} B) {(7, -3)} C) 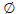D) {(8, -3)}

Solve the problem.
115) Midtown Delivery Service delivers packages which cost $2.40 per package to deliver. The fixed cost to
run the delivery truck is $284 per day. If the company charges $6.40 per package, how many packages
must be delivered daily to make a profit of $76?
A) 118 packages B) 71 packages C) 32 packages D) 90 packages

Solve the problem by writing and solving a suitable system of equations.
116) Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged $150 for
3 days and 300 miles, while Mary was charged $271 for 5 days and 600 miles. What does Best Rental
charge per day and per mile?
A) $29 per day and 21 cents per mile B) $21 per day and 29 cents per mile
C) $28 per day and 22 cents per mile D) $30 per day and 22 cents per mile

Graph the solution of the system.
117) x + 2y ≤ 2
x + y ≥ 0

Identify the base and the exponent for the exponential expression.
118) -(-13)⁶
A) Base: -13, exponent: 6 B) Base: 6, exponent: -13
C) Base: 6, exponent: 13 D) Base: 13, exponent: 6

Use the formula A = P(1 + r)ⁿ to find the amount of money in the bank account described. Use a calculator, and round to the nearest cent.

Solve the problem.
120) Find the volume of the figure.

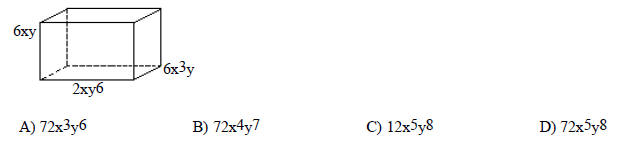
Simplify the expression. Use positive exponents. Assume variables represent nonzero real numbers.

Use the power rules for exponents to simplify. Write the answer in exponential form.

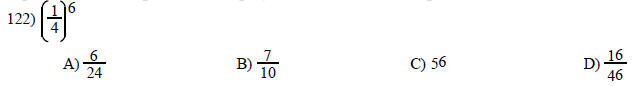
Provide an appropriate response.
123) Decide whether the expression is positive, negative, or zero. 1 - 610
A) Positive B) Zero C) Negative

Evaluate.

Evaluate the expression.

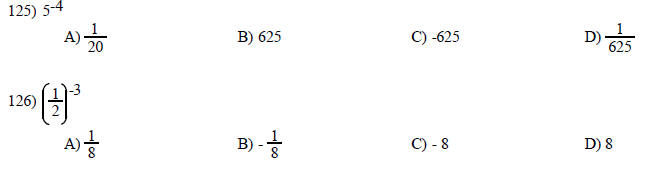
Use a combination of rules for exponents to simplify. Write answers with only positive exponents. Assume that all variables represent nonzero real numbers.

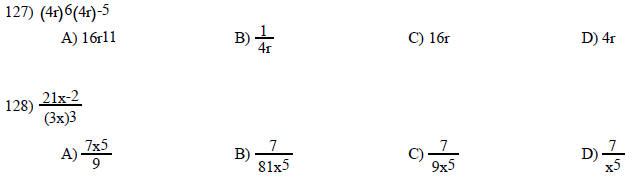
Simplify the expression. Use positive exponents. Assume variables represent nonzero real numbers.

TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false.

Provide an appropriate response.
130) Is it true that in order to multiply a number by a negative power of ten, you must move the decimal point
to the left as many places as indicated by the absolute value of the exponent on the ten?

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

131) In scientific notation, what is the largest integer which can be multiplied by a power of 10?

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question

Determine whether or not the number is written in scientific notation.

If the number in the statement is written in scientific notation, write it without exponents. If it is written without exponents, write it in scientific notation.

134) The population of a small country is 9,347,000 .

Solve the problem. Express the answer in scientific notation to two decimals unless requested otherwise.
135) The national debt of a country is $27,650,000,000 and the population is 5,530,000. What is the debt per
person? Write answer without exponents.
A) $5000 B) $500 C) $50,000 D) $152,904,500

Write the number in scientific notation.
136) .00000039005

Write the number without exponents.

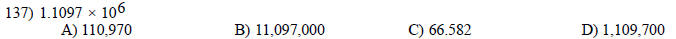
Perform the indicated operation.

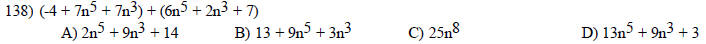
Perform the indicated operations.

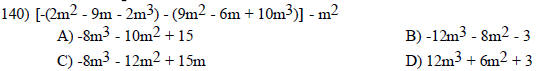
Add or subtract as indicated.

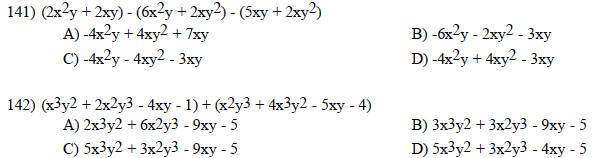
Solve the problem.

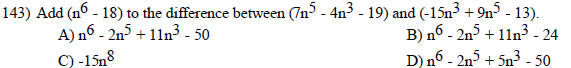
Graph the following by completing the table of values.

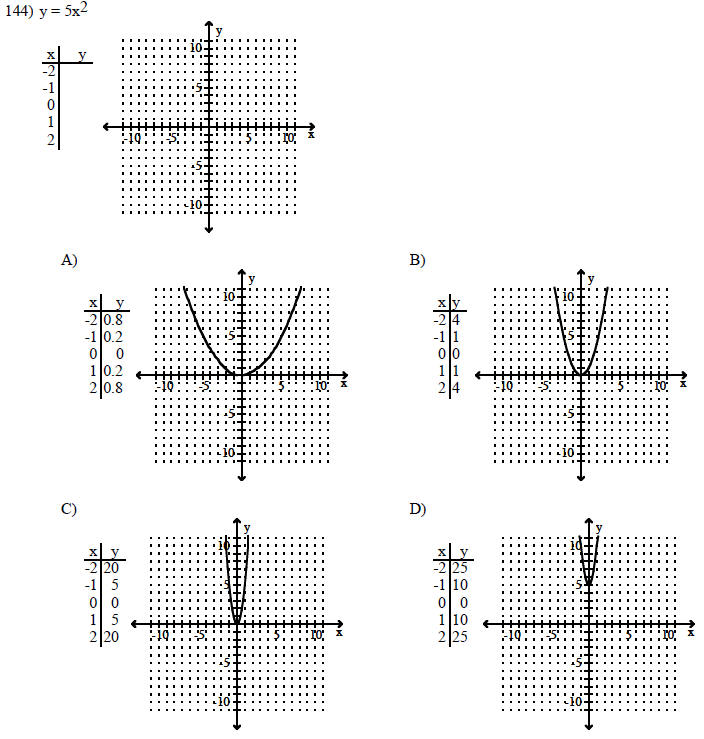
Identify the polynomial as a monomial, binomial, trinomial, or none of these. Give its degree.
145) 5x
A) Monomial, degree 5 B) Monomial, degree 0
C) Binomial, degree 0 D) Monomial, degree 1

Perform the indicated operation.
146) Subtract.

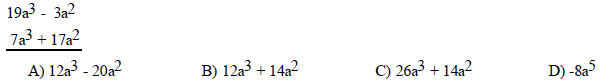
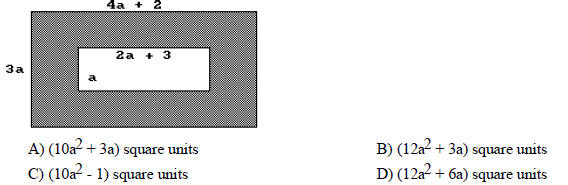
Solve the problem.
147) Determine a polynomial that represents the area of the figure.

148) Find the shaded area.

Find the product.

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Answer the question.
159) Explain how (a + b)^2 differs from a^2 + b^2 by expanding (a + b)^2.

160) Explain how (m - n)^2 differs from m^2 - n^2 by expanding (m - n)^2.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Find the product.

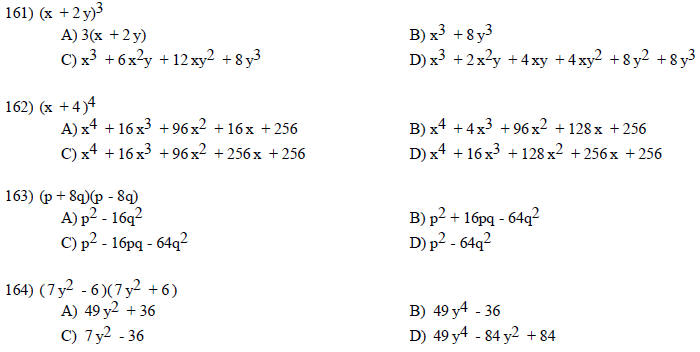
Find the square.

Solve the problem.
166) Determine a polynomial that represents the area of the figure.

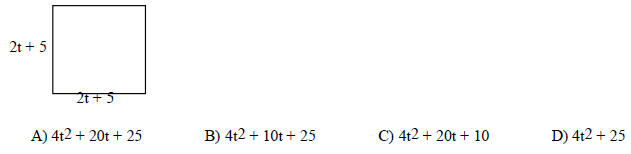
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Answer the question.
167) m and n are natural numbers such that m is less than n. What is the degree of the quotient when a
polynomial of degree n is divided by a polynomial of degree m?

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Perform the division. Write the answer with positive exponents.

Perform the division.

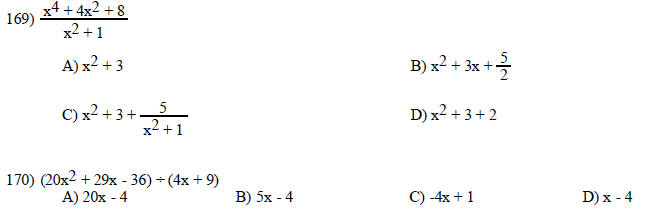
Solve the problem.
171) If a polynomial in x of degree 6 is divided by a monomial in x of degree 4 , what is the degree of the
quotient?
A) 2 B) Can't tell C) 10 D) 4

Factor by grouping.

Complete the factoring.

Factor completely.

Solve the equation.

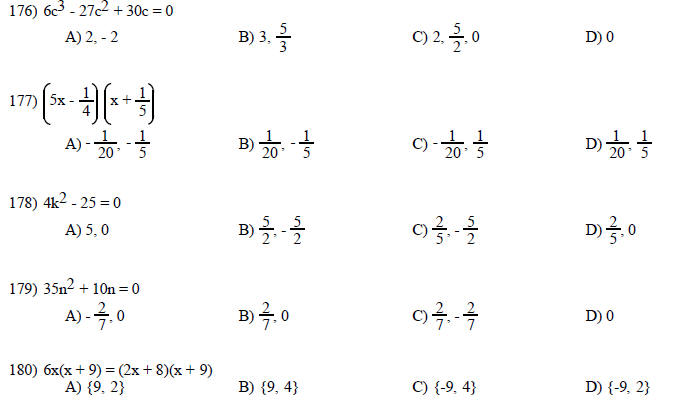
Solve the problem. Round to the nearest tenth, if necessary.
181) If an object is propelled upward from ground level with an initial velocity of 78.6 feet per second, its
height h in feet t seconds later is given by the equation h = -16t² + 78.6t. After how many seconds does
the object hit the ground?
A) 2.5 B) .2 C) 9.8 D) 4.9

Solve the problem.
182) Below is a diagram of a water slide. The slide is 15 ft long. The ladder leading to the slide is 12 ft long.
How far is it from the end of the slide to the foot of the ladder? Round approximations to the nearest tenth.

Find all values that make the expression undefined.

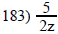
A) None B) 0.5 C) 0 D) 2

Find an expression equivalent to the one given.

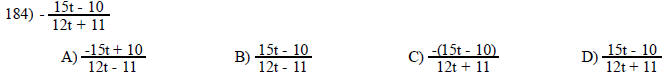
Write the expression in lowest terms.

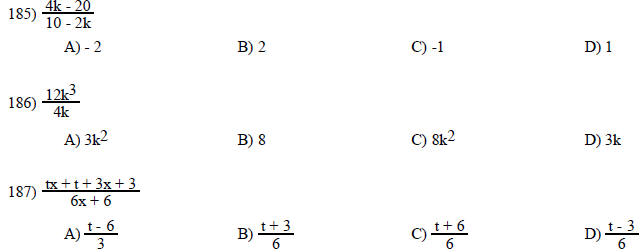
Perform the indicated operation. Write the answer in lowest terms.

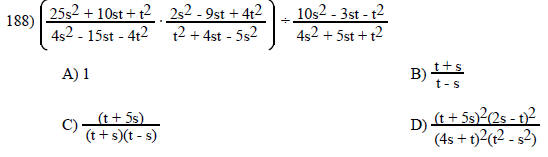
Find the reciprocal.

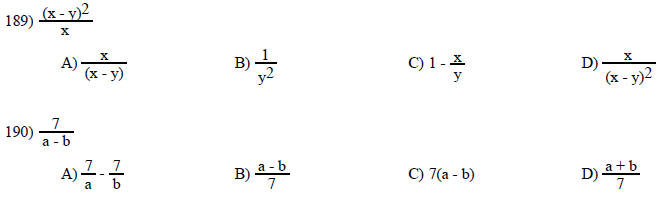
Multiply. Write the answer in lowest terms.

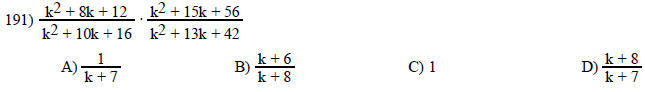
TRUE/FALSE. Write 'T' if the statement is true and 'F' if the statement is false.

Answer the question.
193) If x^e and x^d are denominators of two fractions and e > d , then x^e is the LCD.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question

Find the least common denominator (LCD).

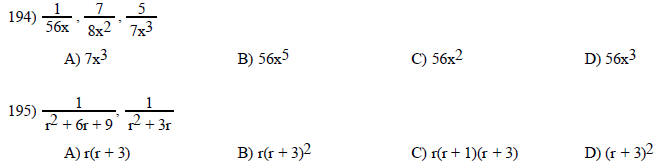
Rewrite the expression with the indicated denominator.

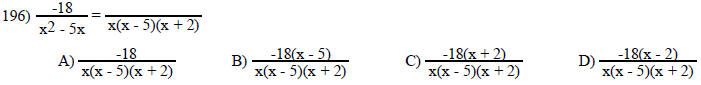
Perform the indicated operation and simplify.

Perform the indicated operation.

Perform the indicated operation and simplify.

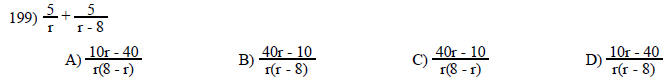
Perform the indicated operation and simplify.

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

Answer the question.
203) What property of real numbers justifies the method of multiplying by the LCD of the parts?
Why?

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

204) Which of the following fractions is equivalent to

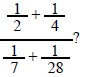
Simplify the complex fraction.

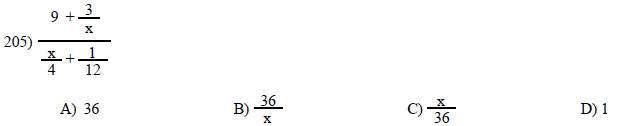
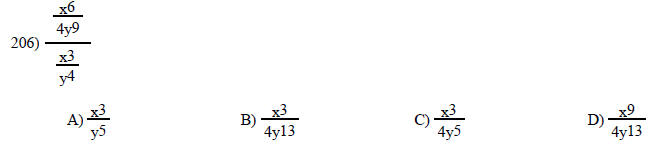
Answer the question.
207) List all numbers that must be rejected as possible solutions.

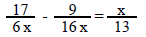
A) There are no numbers that must be rejected. B) { 0 }
C) { 6 , 16 , 13 } D) { 6 , 16 }

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.

208) Explain the difference between adding rational expressions and solving rational equations.

MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.

Solve the equation.

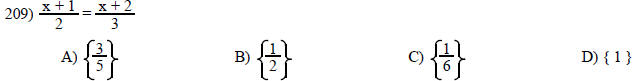
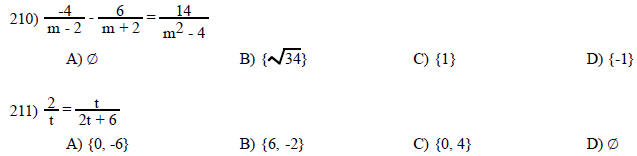
Solve the problem.
212) The winner of the 1998 Peoria 500 (mile) race was Serge Bologna, with an average rate of 121.462 miles
per hour. What was his time in hours? (Round to the nearest one thousandth hour.)
A) 14.117 hours B) -5.883 hours
C) 4.117 hours D) 60,731.000 hours

213) Tom Quig traveled 270 miles east of St. Louis. For most of the trip he averaged 70 mph, but for one
period of time he was slowed to 20 mph due to a major accident. If the total time of travel was 6 hours,
how many miles did he drive at the reduced speed?
A) 60 miles B) 55 miles C) 80 miles D) 70 miles

214) One maid can clean the house in 4 hours. Another maid can do the job in 2 hours. How long will it take
them to do the job working together?