Math 6310 Homework 5

C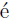sar Lozano

Problem 1 Show that a free group has no elements of finite order. (except e).

Solution. Consider an element a ∈F(S). This means that

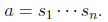
We may assume this is a reduced word. Suppose such a element has order two:

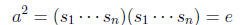
Since a is reduced, then this fact gives relation to the group, as s_ns₁ = e for instance. Then
a ∈ F(S) cannot have order two. We can argue the same for

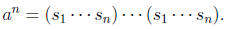
If we have aⁿ = e we got group relations s_ns₁= e and therefore the group F(S) is no longer
free. Therefore, an element a ∈ F(S) may not have finite order.

Problem 2 A Boolean ring is a ring R such that x^2 = x for all x ∈ R. If R is a boolean
ring, show that

•x = -x for all x ∈ R

•R is commutative.

Solution. The firs statement is equivalent to 2x = 0 for all x ∈ R

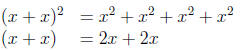
This show that 2x = 0.

Now, in order to prove the second statement, just look the following computation

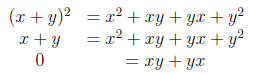
Taking into account in the last equation that x = -x, we have xy = yx, as desired.

Problem 3 Show that the only homomorphism from R to R is the identity.

Solution. First, let f : R -> R be a ring homomorphism. Consider n ∈ N, then

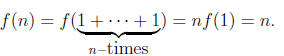
Thus the restriction f|Z is the identity map. Now consider n ∈ Q, this means we can write

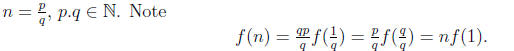
Then we can conclude that the map is the identity map on the rational number Q.

Observe that if x > 0, there exits positive number y^2 = x such that f(x) = f(y)f(y) > 0.
As a result we have, if x - y > 0 then

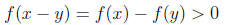
In other words, if x < y, implies f(x) < f(y).

Now consider {x_n} a sequence of rational numbers converging to r ∈ R,Q.
We can assume this since Q is dense in R. Then for each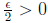
there exist N ∈ N such that

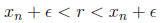
however applying f to this inequality, we may have

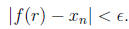
Therefore, the function f(r) is the identity on R as desired

Problem 4

Solution. From now on, consider an arbitrary element y ∈ R.

•Multiplicative closure. Consider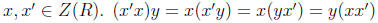

•Additivity closure. Consider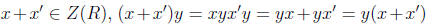

•Additive Inverses. Consider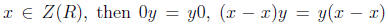 this implies

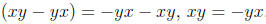
Problem 5 Let S be a multiplicative set in a commutative ring R and let I be an ideal
maximal with respect to the property that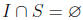Show that I is prime.

Solution. If f,g ∈ R are not in I, then by the maximality of I, both I +(f) and I +(g)
meet S. Thus, there are elements of the form af + r and bg + s in S such that r, s ∈ I. If
fg ∈ I, the the product of af + r and bg + s would be in I, contradicting the fact that I
does not meet S

Problem 6 If R is an integral domain that is not a field, show that R[x] is not a principal
domain.

Solution. Observe that in a principal ideal domain R, each prime ideal is maximal. This
fact is due to if 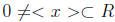and there is 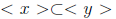then x = ty. Further ty ∈< x >
where 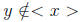then t = rx. Therefore x = rxy which means 1 = ry because R is integral
domain. Therefore, < y >= R.

Keeping this argument in mind, suppose R an principal domain. Thus we have that < x >
is maximal. However, the quotient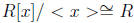 is not a field, which is a contradiction.

Problem 7 Let R a commutative ring and let G be a group. Let R[G] be the group ring.
The augmentation ideal of R[G] is the kernel of the homomorphism from R[G] to R that sends

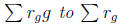
Show that the augmentation ideal is generated by the elements g - e for g ∈ G.

Solution. Thus, certainly the elements of the form {(x - e) : x ∈G} are in the kernel.
Now we want to see the kernel is generated by only those elements. Note that if a₁x₁ + … +
a_nx_n -> 0 this implies that a₁ + … + a_n = 0. It is clear that a₁(x-e) + … + a_n(x_n - e) goes
to zero as desired.

Problem 8 Let p a prime number, and let R be a commutative ring such that pr = 0 for all
r ∈R. Show that the function form R to R that sends r to r^p is a ring homomorphism.

Solution. First, observe that p prime number implies that

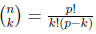
has always p as a factor. Therefore,

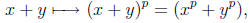
since px = 0. Moreover

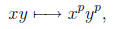
since R is a commutative ring. As a result the map x -> x^p is a ring homomorphism.