- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Math Problems
Mathematics Contained in these Three Lessons
"Reading This Could Help You Sleep: Caffeine in Your Body" is an
introduction to
exponential functions of the form 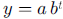 at the
Intermediate Algebra level, with
at the
Intermediate Algebra level, with
emphasis on the meaning of these functions and their graphs. The concept of
half-life is
introduced. A conditional function (a piecewise-defined function) is used.
"Get the Lead Out" extends the study of exponential functions and can be used to
introduce the use of logarithms to "un-do" exponential expressions in solving
equations.
"So Much Coffee, So Little Time" can be used at the Intermediate Algebra level
to
help students see the value of "solving systems of linear equations". It shows
connections
between solving linear equations and exponential functions, and continues the
study of
exponential functions this time of the form 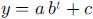 .
End behavior of these
.
End behavior of these
functions with horizontal asymptotes is included.
Set-up
Each students should have a graphing calculator. Alternatively, each group of 4
students should work at one computer.
Organization
These three lessons are interdependent. They should be done in the ordered
listed
above in the title to the Teacher Materials. You can do the first without doing
the second
or the third, or you can do the first and second without doing the third. We
recommend
that you not try to use the second or third unless you have done the one(s) that
precede it.
Each unit can be used at a time that is appropriate for the course, that is,
they do not need
to be covered on consecutive class days.
Answers to Problems and Teaching Suggestions for Reading This Could Help You
Sleep: Caffeine in Your Body
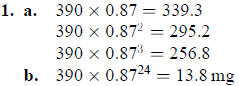
Reflection Point: Students should have attempted problem 1 for homework.
You can
begin class by discussing the reading and the students' answers. When you
discuss this
homework problem in class, have students describe how they actually computed the
answers for part a. Be sure that all students see the relationship between
multiplying
again by 0.87 and increasing the exponent on 0.87 by 1. Having different
students
explain their reasoning for problem 1b in class should help all students
understand the
process. After the discussion, hand out Eliminating Caffeine from the
Body, page 3 of
this activity, and have the students work on this page in groups of 3 or 4.
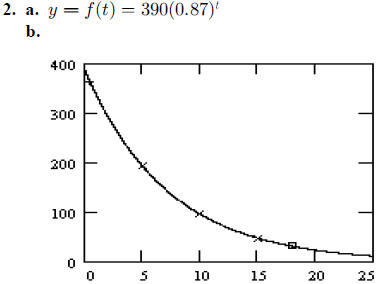
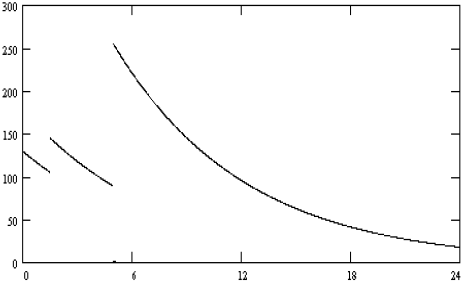
c. As t gets large, 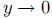
d. This point is at about 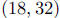 and is shown with
a box in the graph.
and is shown with
a box in the graph.
e. When 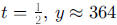 . This point is shown with a + on the
graph.
. This point is shown with a + on the
graph.
Students can get this result approximately from their graphs. You might wish to
remind
students that an exponent of 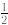 indicates a
square root. If so, they can calculate
indicates a
square root. If so, they can calculate
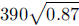 and compare with their reading from the
graph.
and compare with their reading from the
graph.
f. When 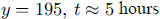 .
.
g. After two half-lives, 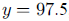 , which is
, which is
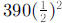 ;after three half-lives,
;after three half-lives,
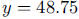 ,
,
half of the previous result 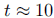 hours is two
half-lives; three half-lives is
hours is two
half-lives; three half-lives is
approximately hours.
Students can get these results approximately from their graphs. Help them
recognize that
after each 5 hour period (approximately), the amount of caffeine remaining in
the body is
about half what it was at the beginning of the 5-hour period. Studying the graph
with
this in mind will help to prepare students for later work with half-life. These
three points
are marked with × on the graph.
Homework
Problem 3 is intended to extend students' familiarity with exponential
functions.
Each person's table and graph will differ from the others, of course, but we
suppose most
will have more than one drink during the day containing caffeine. In this case,
most will
have to write a conditional function. For a person who consumes130 mg at 8:00
am, 40
mg at 9:30 am, and 165 mg at 1:00 pm, the conditional function could be written
as
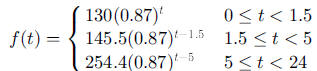
or as
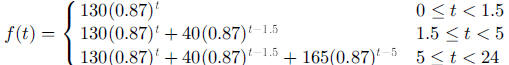
where t measures time in hours after 8 am. Since the
person in our table had her first cup
of coffee at 8 am, she measures t in hours since 8 am. Thus, after 9:30 am, she
will need
to use 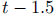 as an exponent to indicate hours that
have passed since her 9 am Dr.
as an exponent to indicate hours that
have passed since her 9 am Dr.
Pepper and later, 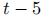 as an exponent to indicate
hours that have passed since her 1pm
as an exponent to indicate
hours that have passed since her 1pm
espresso. Note that in the first form of the function, the total amount of
caffeine in the
person present at time 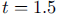 and
and
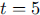 was computed and used to start the next
was computed and used to start the next
exponential. In the second form of the function, the caffeine in each drink is
considered
as being eliminated exponentially and independently from the caffeine in the
other drinks.
To graph such a function on a graphing calculator, set the calculator to DOT
mode
(as opposed to CONNECTED) to avoid lines joining endpoints. The function can be
graphed several different ways. For example, students could graph
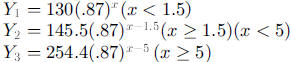
or
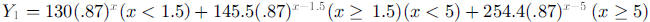
or 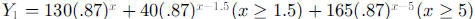
with the window set for 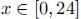 and
and
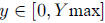 with max depending on the
with max depending on the
student. The graph should look something like the following graph.
Answers to Problems and Teaching Suggestions for Get
the Lead Out
1. a. 0.9850, 0.9702, 0.9557, 0.9413 mg, respectively
b. 7 days
c. 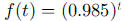
Reflection Point: It is assumed students will have worked problem 1 for
homework. If
you discuss this homework problem in class, ask students how they did the
problems.
You might then note that the answer to part b is the approximate solution to the
equation
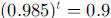 and discuss how you could use this equation
to find t; that is, take the log
and discuss how you could use this equation
to find t; that is, take the log
of both sides. If you plan to teach solution of exponential equations "by hand",
now is a
good time to help students recognize the need for an inverse for exponential
functions
with which to do it. The equations can be solved using a graphing utility, of
course, but if
students try that method first, they will be ready to recognize that the search
for an
appropriate window for a solution to these equations may not be as fast or as
easy as a
logarithmic approach.
After discussing problem 1, you should hand out Get the Lead Out
Classroom
materials and have students work on problems 2 and 3 in groups of 3 or 4. You
can also
have them work on problem 4 on page 3 of this activity, or you can assign that
problem
for homework.
2. a. 1.9700, 1.9404, 1.9113 mg, respectively
b. 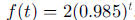 After 46 days (or 45.862), the
amount of lead in her body will be
After 46 days (or 45.862), the
amount of lead in her body will be
reduced to 1 mg.
If students have any difficulty answering part b, ask them to explain how they
worked
part a. Remind them about the caffeine activity. Help them generalize for any
and then
recognize that the function is exactly that generalization. The determination of
half-life
can be found from the graph or by taking the log of both sides of the equation
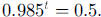 Discussion to review the term half-life
would be helpful here.
Discussion to review the term half-life
would be helpful here.
c. Another 46 days.
Here you might also show students another form of the function based on the
half-life
idea: 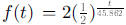 It might help them understand this if
they use their calculator to
It might help them understand this if
they use their calculator to
see that
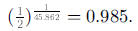
d. The half-life is 45.862 days. This means that every 45.862 days, half of the
lead is
eliminated from the blood.
e. To a level of 0.4 mg: 106.5 days. To a level of 0.2 mg: another 46 days, or
45.862 -
thus about 152 days.
For the 0.4 mg question, students might use their graphing calculators or they
might
calculate using logarithms. To answer the 0.2 mg question, they have many
choices,
but we hope they will use the half-life idea of part d.
3. 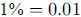 one hundredth of
one percent is
one hundredth of
one percent is 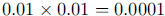 Be aware of the
Be aware of the
potential for error here. Misunderstanding of this decimal will lead students
far astray
on the rest of the problem!
a. 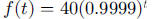
b. 18.989 or 19 years; 37.9788 or 38 years
c. 18.989 or 19 years
Reflection point: This is a good time to ascertain that students
understand half-life.
4. a. If 0.02% of the cadmium is removed from the body each day, it will take
about
3465 days, or 9.49 years. The easiest way to find this is to solve
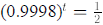 .If
.If
0.004 % of the cadmium is removed from the body each day, it will take about
17328 days, or 47.47 years, which can be found by solving
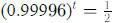 So the
So the
half-life for cadmium is between 9.5 and 47.5 years, depending on the person.
Answers to Problems and Teaching Suggestions for So
Much Coffee, So Little Time:
More on Caffeine in the Body
This activity can be used to help students see the value of "solving systems of
linear equations" at the Intermediate Algebra level. It shows connections
between solving
linear equations and exponential functions; that is, we need to use a number of
different
mathematical concepts to analyze real problems.
1. After n cups, t hours after the first cup, there will be f(t) grams of
caffeine in the
body.
| n cups | hours | mg of caffeine in body |
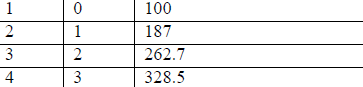 |
||
2. Solve 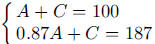 to get
to get
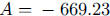 and
and 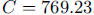 Graph
Graph
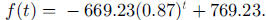
It will be seen from the graph that this function is monotone increasing and its
end
behavior is to approach the line 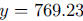 , although
students may not recognize
, although
students may not recognize
immediately that the asymptote is exactly the constant term of the function.
From this
information, students can conclude that no one will die of an overdose of
caffeine, which
would happen at a level of about 5000 mg, by drinking 1 cup of coffee per hour.
Reflection point: Students should have attempted problems 1 and 2 for
homework. At
the beginning of class, initiate a whole-class discussion to be sure students
understand the
form of this exponential function, 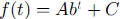 ,
why this one (with
,
why this one (with 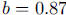 ) does
) does
not go off to infinity, and how they might have known what its horizontal
asymptote
would be from looking at the equation. One result of this example is that the
amount of
caffeine stabilizes at an equilibrium value of 769.23 mg in the body. Discuss
this result
with students in relation to medicines which are given periodically; that is,
that the
amount of medicine in the body stabilizes at a level deemed appropriate by the
physician.
Pass out Smokin' and have the students work on problems 3, 4, and 5 in
groups.
3. a. Solve 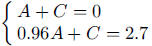 to get
to get
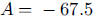 and
and 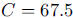 .
Thus, the function
.
Thus, the function
is 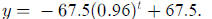
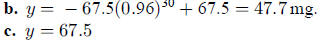
Assure that students see this result geometrically (on
their graphs) and algebraically
(from studying the function). It would also be valuable to see it numerically
from an
electronically generated table.
4. a. The amount absorbed each year is
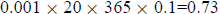 , so
, so 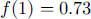 .
.
Also, 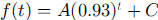 , so students need to solve the
equations
, so students need to solve the
equations
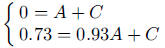
giving 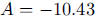 and
and
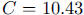 , so
, so 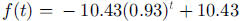 and
and
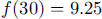 mg of cadmium.
mg of cadmium.
b. The amount absorbed each year is 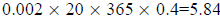 , so
, so
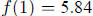
Also, 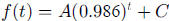 , so students need to solve the
equations
, so students need to solve the
equations
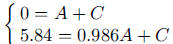
giving 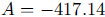 and
and
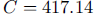 so
so 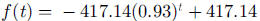 and
and
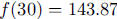 mg of cadmium.
mg of cadmium.
5. 47.7 (our result in problem 3) is about 1.6 times the "average." In order to
assess the
relationship between our result that the smoker receives 47.7 mg more cadmium as
a
result of smoking and the "average" amount of 30 mg, we would need to know what
proportion of the 50 year old population has smoked for 30 years and what is the
average number of cigarettes smoked per day. We would also need to know for how
long and at what ages other fractions of this population smoked. That the added
amount due to cigarettes is actually between about 10 mg and about 150 mg makes
it
even harder to assess the validity of this statement. There is no right or wrong
answer
to this problem. Hopefully it will cause students to think more deeply about the
math
and about what additional information might be needed before making a statement
like
that given in this problem.


