Quadratic Equations

Quadratic Equation: Eqn equivalent to

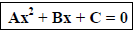
where A, B, C real, A ≠ 0
This 2^nd degree eqn is the standard form.

Solving by Factoring
If can factor left side, then can solve by Zero-
Product Property which says:
If ab = 0 then either a = 0 or b = 0 or both

In general, quadratic eqn has 2 roots.
If both factors in factorization are identical,
both solns same & root has multiplicity 2,
called double root.

e.g.

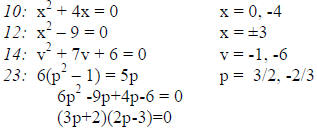
Square Root Method
Some eqns solved simply by taking square root
e.g. If x² = p and p ≥ 0, then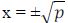

e.g.

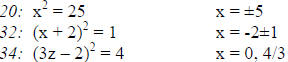
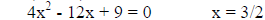(double root)

Completing the Square
If left side of eqn is perfect square, can solve it.
Adjust left side to be perfect square, change right
side appropriately

e.g.
42: x² – 6x = 13

Strategy:
If x² has coefficient ≠ 1, divide both sides by it
Start with x² + Bx + C = 0
Move C to other side x² + Bx = C
Add 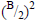to both sides
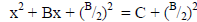
Use Square Root Method to solve eqn.
e.g.
46: 2x² – 3x – 1 = 0
 

Quadratic Formula
For general quadratic (with A ≠ 0)
ax² + bx + c = 0

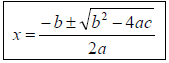
Discriminant: (b² – 4ac)
If (b² – 4ac) > 0 then 2 real solutions
If (b² – 4ac) = 0 then 1 real solution
If (b² – 4ac) < 0 then no real solutions

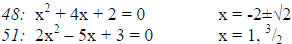
53: 4y² – y + 2 = 0no real solns
59: 9t² – 6t + 1 = 0 x = 1/3 (double root)

Assignment:
Do problems for 1.2
Read §1.3