- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Rationalize Denominators
| Rationalize Denominators MATH 018 Combined Algebra S. Rook |
| Overview • Section 10.5 in the textbook: – Rationalizing a denominator with one term – Rationalizing a denominator with two terms |
| Rationalizing Denominators with One Term |
| Rationalizing Denominators with One Term • Rationalizing: the process of eliminating the radical from either the numerator or denominator of a fraction – We will only be rationalizing the denominator Consider 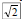 – what happens when we
multiply – what happens when we
multiply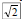 by itself? by itself? |
• Thus, we can say: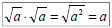 • To rationalize a denominator with one term: – Determine what needs to be multiplied to eliminate the radical in the denominator – Multiply this term times BOTH the numerator and denominator (dealing with an expression) • This eliminates the radical in the denominator – Acceptable to have radicals present in the numerator |
| Simplify Radicals Before Rationalizing • Consider rationalizing 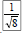 – Could multiply numerator and denominator by 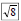 – Easier, however to simplify 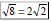 • Multiply numerator and denominator by instead of 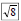 • See if radicals can be simplified before rationalizing – Otherwise radicals must be simplified at the end where the numbers are larger |
| Rationalizing Denominators with One Term (Example) Ex 1: Rationalize the denominator:  |
| Rationalizing Denominators with Two Terms |
| Rationalizing Denominators with Two Terms • Again, goal is to eliminate the radicals from the denominator – Consider 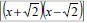 – Consider 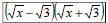 |
| • Conjugate: same 2 terms but different signs – Given 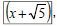 , what would be its
conjugate? , what would be its
conjugate?• To rationalize a denominator with two terms: – Multiply BOTH the numerator and denominator by the conjugate (dealing with an expression) • Eliminates the radical(s) in the denominator – Acceptable to have radicals present in the numerator • Look to simplify radicals before rationalizing |
Ex 2: Rationalize the denominator: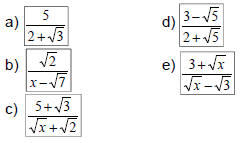
|
| Summary • After studying these slides, you should know how to do the following: – Rationalize denominators containing one or two terms • Additional Practice – See the list of suggested problems for 10.5 • Next lesson – Solving Radical Equations (Section 10.6) |


