Some Proofs of the Existence of Irrational Numbers

Neal Coleman is a freshman majoring in pure math- ematics at Ball State. He served as the secretary of the Ball State Math Club during the 2006-07 school year; during the fall semester, he participated in the Student-Faculty Colloquium, where, advised by Dr. Rich Stankewitz, he prepared a presentation on proofs of the existence of irrational numbers.

Over the course of this article, we will discuss irrational numbers and several
different ways to prove their existence. As is commonly known, the real num-
bers can be partitioned into rational numbers and irrational numbers. Rational
numbers are those which can be represented as a ratio of two integers — i.e.,
the set {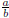: a, b ∈ Z, b ≠ 0} — and the irrational numbers are those which
cannot be written as the quotient of two integers. We will, in essence, show
that the set of irrational numbers is not empty. In particular, we will show ,
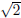e, π, and π² are all irrational.

Geometric Proof of the Irrationality of

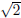
The ancient Greeks were some of the first mathematicians. However, instead
of approaching mathematical problems numerically or abstractly, the Greeks
were very concrete: they envisioned problems geometrically. They considered
numbers to be analogous to line segments. Two segments are considered commensurate
if and only if there exists some other segment called a "common
measure" which can be overlaid an integer number of times onto both. That is
pretty convoluted; it is easier to think of two segments as commensurate when
you can find some other "unit" segment to measure them both, where each has
integer length with respect to the segment of this "unit.

We begin by discussing why the diagonal and side of a square are incom-
mensurate, i.e., why it is impossible to find some segment, however small, that
can measure both the diagonal and square.

We start our proof from [2, p. 23], by constructing a square ABCD. Because
we are assuming the side and diagonal are commensurate for contradiction, we
shall denote the segment of common measure between the side AD and the
diagonal AC by e. To begin the proof, on the diagonal AC, starting from C,
measure out a segment congruent to AD 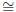CD, and call the point where the
subsegment terminates F. Next construct a line perpendicular to AC from F
out to AD. Call the point where it meets the side B'. Note that because angle
B'AF is 45° and AFB' is 90°, AF 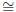B'F. Moreover, ΔCF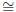B' ΔCDB'
because both are right triangles, CD 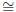CF, and they share the hypotenuse
CB'. We may therefore conclude that B'D 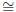B'F 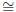AF. Now, create a new
square with B'F and FA as sides. Note that the new diagonal is going to be
B'A. Since AC and FC 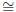CD 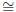AD are commensurate by e, then so are AF
and B'A, one side of the new square and its diagonal.

Clearly, we can repeat this process of constructing a new square indefinitely,
with each new square strictly smaller than the last. Note also that, inductively,
the sides and diagonal of each new square are measured by our original e. This
is a contradiction by infinite descent: for example, suppose that |AC| = 1000e;
since each successive diagonal is measurable by e, and we can construct a
new diagonal indefinitely, the 1001st diagonal we construct will no longer be
commensurate by e.

We conclude that the side and diagonal of a square are incommensurable.
This is equivalent to stating that is irrational: two line segments are com-
mensurable if and only if there exists another segment such that each of the
two initial segments is an integer multiple of that third one, i.e., that the ratio
of their lengths can be represented as a rational number. Hence, since the
diagonal and side of a square are incommensurable, their ratio, , cannot be
represented as a ratio of two integers, and is therefore irrational. Incidentally,
it is to be noted that the discovery of irrational numbers shocked and startled
the Greeks: according to legend, the Pythagorean who first completed this
proof atoned by perishing in a shipwreck [2].

Algebraic Proof of the Irrationality of

We can take the essence of the geometric proof presented above and distill it
into an algebraic argument as follows.

To prove the irrationality of by contradiction, we suppose it is rational.
Then consider the set 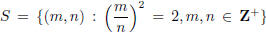. Invoking the
Well-Ordering Principle, set 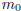= min{m : (m, n) ∈ S}, the smallest of the set
of numerators. Then let 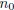∈ be the matching denominator for such
that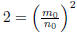, and thus 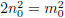. Now, we have, by subtracting 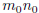from
both sides, 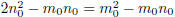; that is,

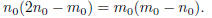
And so

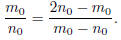
Since > 1, we know 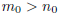; however, this implies that 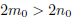, which
indicates that 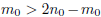. This is a contradiction to the minimality of ,
establishing that is irrational.

The basic idea behind these first two proofs is to find some violation of the
Well-Ordering Principle: to show that if were rational, it would be possible
to construct a set of positive integers with no smallest element (in the first
proof, this set with no lower bound is the set of diagonals: they are integer
multiples of finite e, and yet can decrease indefinitely; in the second proof, and
a bit more explicitly, the set with no lower bound is the set of all numerators
of rational realizations of ).

It should be noted that the commonplace proof of the irrationality of
invokes the Prime Factorization theorem in order to have the phrase "reduced-
form fraction" be well-defined; the two proofs presented above, however, do
not require this secondary result, and so are somewhat stronger than the most
common proof.

Irrationality of e

The number is not, of course, the only irrational number; it is possible
to show that some important numbers which naturally occur in geometry and
analysis are also irrational. For example, as seen in [1], let us consider the
natural exponential e. Given the MacLaurin expansion of e^x, we see that

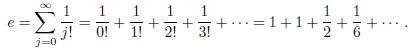
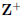Suppose for contradiction that e = is rational, with a, b ∈ . Now, fix any
k > 1 such that b|k!, for example, k = b.

Define

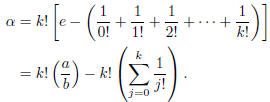
Thus, because both terms in the final expression are integers, α ∈ Z. But
consider now that

Since k > 1, we now have a startling and unsettling occurrence: the integer α
satisfies 0 < α < 1. This is our contradiction: e is therefore irrational.

Irrationality of π and π²

Nearly as ubiquitous as e, but arising initially from geometric instead of analytic
considerations, is the number π, the ratio of any circle's circumference to its
diameter. This last proof (from [1, pp. 46–47], with some detail added), of
the irrationality of π, is rather more mysterious than the previously discussed
proofs. Several very conveniently chosen functions conspire to show that it is
impossible to write π or π² as quotients of integers.

We begin by defining, for any positive integer n,

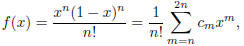
where the 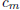∈ Z. Note that for 0 < x < 1, we have 0 < f(x) < 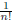and that
f(0) = 0 and 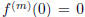if m < n or m > 2n. However, if n ≤ m ≤ 2n,
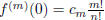∈ Z.

Hence, f(x) and all its derivatives take integral values at x = 0. Since
f(1-x) = f(x), the same is true at x = 1, because.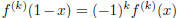

Now, suppose that π² = is rational, where a and b are positive integers.

Consider the function



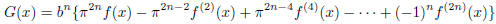
Note that both G(0) and G(1) are integers. With a little algebra, we have

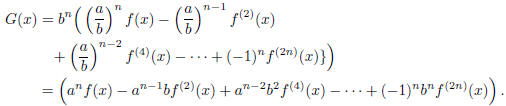
Then

Therefore,

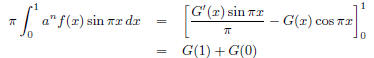
which is an integer. But, because 0 < f(x) < , for any x such that 0 < x < 1,

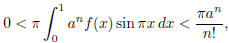
which is strictly less than 1 for large n.
This is our contradiction. Consequently, π² is irrational, and so is π.

References

[1] G.H. Hardy, and E.M. Wright, An Introduction to the Theory of Numbers,
Oxford University Press (1979).
[2] H. Rademacher, and O. Toeplitz, The Enjoyment of Mathematics, Dover
(1990).