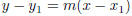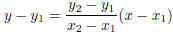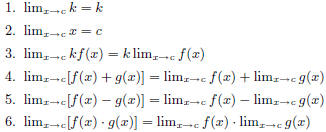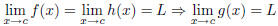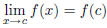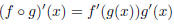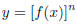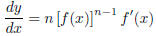- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Calculus Term Definitions
| Copyright & License Copyright c 2007 Jason Underdown Some rights reserved. Calculus I |
Formula quadratic formula Calculus I |
|||||||||||||||
| Definition absolute value Calculus I |
Theorem properties of absolute values Calculus I |
|||||||||||||||
| Definition equation of a line in various forms Calculus I |
Definition equation of a circle Calculus I |
|||||||||||||||
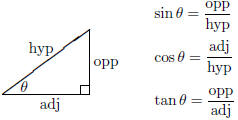
| Definition sin, cos, tan Calculus I |
Definition sec, csc, tan, cot Calculus I |
|||||||||||||||
| Definition midpoint formula Calculus I |
Definition function Calculus I |
|||||||||||||||
| The solutions or roots of the quadratic equation ax2 + b x + c = 0 are given by  |
These flashcards and the accompanying
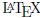 source
sourcecode are licensed under a Creative Commons Attribution–NonCommercial–ShareAlike 2.5 License. For more information, see creativecommons.org. You can contact the author at: jasonu at physics utah edu File last updated on Sunday 8th July, 2007, at 17:15 |
|||||||||||||||
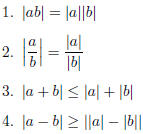 |
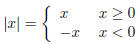 |
|||||||||||||||
| The equation of a circle centered at (h, k) with
radius r is: (x − h)2 + (y − k)2 = r2 |
|
|||||||||||||||
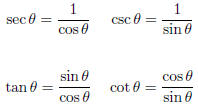 |
 |
|||||||||||||||
| A function is a mapping that associates with each object x in one set, which we call the domain, a single value f (x) from a second set which we call the range. |
If P(x1, y1) and Q(x2, y2) are two points, then
the midpoint of the line segment that joins these two points is given by: 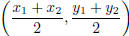 |
|||||||||||||||
| Definition even and odd functions Calculus I |
Definition limit Calculus I |
|||||||||||||||
| Definition one–sided limit Calculus I |
Theorem limit exists iff both the right–handed and left–handed limits exist and are equal Calculus I |
|||||||||||||||
| Theorem main limit theorem (part 1) Calculus I |
Theorem main limit theorem (part 2) Calculus I |
|||||||||||||||
| Theorem squeeze theorem Calculus I |
Theorem two special trigonometric limits Calculus I |
|||||||||||||||
| Definition point-wise continuity Calculus I |
Theorem composition limit theorem Calculus I |
|||||||||||||||
| If a function f (x) is defined on an open interval
containing c, except possibly at c, then the limit of f (x) as x approaches c equals L is denoted 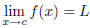 The above equality holds if and only if for any  there exists 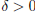 such that such that |
even f(−x) = f (x) for all x e.g. x2, cos (x) odd f(−x) = −f (x) for all x e.g. x, sin (x) |
|||||||||||||||
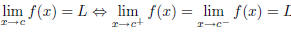 |
right–handed limit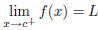 iff for any 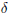 such that such that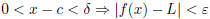 |
|||||||||||||||
| Let f, g be functions that have limits at c, and
let n be a positive integer. 7. 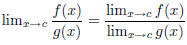 if if
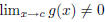 8. 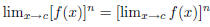 9. 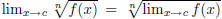 provided that provided that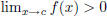 when n is even. when n is even. |
Let k be a constant, and f, g be functions that
have limits at c.
|
|||||||||||||||
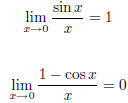 |
Suppose f, g and h are functions which satisfy
the inequality 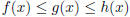 for all x near c, (except for all x near c, (exceptpossibly at c). Then
|
|||||||||||||||
If 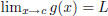 and f is continuous at L, then and f is continuous at L, then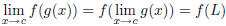 |
Let f be defined on an open interval containing
c, then we say that f is point-wise continuous at c if
|
|||||||||||||||
| Definition continuity on an interval Calculus I |
Definition derivative Calculus I |
|||||||||||||||
| Definition equivalent form for the derivative Calculus I |
Theorem differentiability and continuity Calculus I |
|||||||||||||||
| Theorem constant and power rules Calculus I |
Theorem differentiation rules Calculus I |
|||||||||||||||
| Theorem derivatives of trig functions Calculus I |
Theorem chain rule Calculus I |
|||||||||||||||
| Theorem generalized power rule Calculus I |
Definition notation for higher-order derivatives Calculus I |
|||||||||||||||
| The derivative of a function f is another
function f' (read “f prime”) whose value at x is 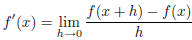 provided the limit exists and is not ∞ or −∞. |
function f is said to be continuous on an open inteval iff f is continuous at every point of the open interval. A function f is said to be continuous on a closed interval [a, b] iff 1. f is continuous on (a, b) and 2. 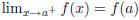 and and3.  |
|||||||||||||||
| If the function f is differentiable at c, then f
is continuous at c. |
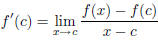 |
|||||||||||||||
| Let f and g be functions of x and k a constant. 1. scalar product rule (k f)' = k f' 2. sum rule (f + g)' = f' + g' 3. difference rule (f − g)' = f' − g' 4. product rule (f g)' = f' g + f g' 5. quotient rule  |
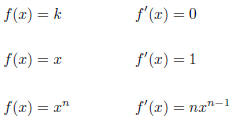 |
|||||||||||||||
| Let u = g (x) and y = f (u). If g is differentiable
at x, and f is differentiable at u = g (x), then the composite function 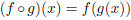 is differentiable at x and is differentiable at x and
In Leibniz notation
|
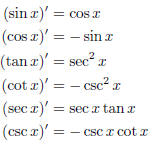 |
|||||||||||||||
|
If f is a differentiable function and n is an
integer, then the power of the function
is differentiable and
|
|||||||||||||||
| Theorem extreme value theorem Calculus I |
Theorem intermediate value theorem Calculus I |
|||||||||||||||
| Definition critical point stationary point singular point Calculus I |
Definition increasing decreasing monotonic Calculus I |
|||||||||||||||
| Theorem monotonicity theorem Calculus I |
Definition concave up concave down Calculus I |
|||||||||||||||
| Theorem concavity theorem Calculus I |
Definition inflection point Calculus I |
|||||||||||||||
| definition local maximum local minimum local extremum Calculus I |
Theorem first derivative test Calculus I |
|||||||||||||||
| If the function f is continuous on the closed
interval [a, b] and v is any value between the minimum and maximum of f on [a, b], then f takes on the value v. |
If the function f is continuous on the closed
interval [a, b], then f has a maximum value and a minimum value on the interval [a, b]. |
|||||||||||||||
| A function f defined on the interval I is • increasing on I , for every  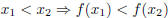 • decreasing on I , for every 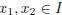 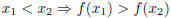 The function f is said to be monotonic on I if f is either increasing or decreasing on I. |
If f is a function defined on an open interval
containing the point c, we call c a critical point of f iff either • f' (c) = 0 or • f' (c) does not exist Furthermore when f' (c) = 0 we call c a stationary point of f, and when f' (c) does not exist we call c a singular point of f. |
|||||||||||||||
| Suppose f is differentiable on an open interval
I, then if f' is increasing on I we say that f is concave up on I. If f' is decreasing on I we say that f is concave down on I. |
Suppose f is differentiable on an open interval
I, then • f' (x) > 0 for each 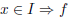 is increasing on I is increasing on I• f' (x) < 0 for each 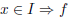 is decreasing on I is decreasing on I |
|||||||||||||||
| Let f be continuous at c, then the ordered pair
(c, f (c)) is called an inflection point of f if f is concave up on one side of c and concave down on the other side of c. |
Let f be twice differentiable on the open
interval I. • f'' (x) > 0 for each 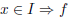 is concave up on I is concave up on I• f'' (x) < 0 for each 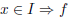 is concave down on I is concave down on I |
|||||||||||||||
| Let f be differentiable on an open interval (a,
b) that contains c. 1. 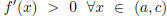 and and
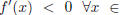  is a local maximum of f. is a local maximum of f.2.  and and
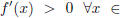  is a local minimum of f. is a local minimum of f.3. If f' (x) has the same sign on both sides of c, then f (c) is not a local extremum. |
Let the function f be defined on an interval I
containing c. We say f has a local maximum at c iff there exists an interval (a, b) containing c such that f (x)≤ f (c) for all x ∈ (a, b). We say f has a local minimum at c iff there exists an interval (a, b) containing c such that f (x) ≥f (c) for all x ∈ (a, b). A local extremum is either a local maximum or a local minimum. |
|||||||||||||||
| Theorem second derivative test Calculus I |
Theorem mean value theorem Calculus |
|||||||||||||||
| If f is continuous on a closed interval [a, b]
and differentiable on its interior (a, b), then there is at least one point c in (a, b) such that 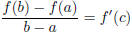 or equivalently f (b) − f (a) = f' (c)(b − a) |
Let f be twice differentiable on an open interval
containing c, and suppose f' (c) = 0. 1. If f'' (c) < 0, then f has a local maximum at c. 2. If f'' (c) > 0, then f has a local minimum at c. 3. If f'' (c) = 0, then the test fails. |
|||||||||||||||