WRITTEN HOMEWORK ASSIGNMENT

KEVIN YOKOYAMA

Abstract. Digital signal processing is concerned with processing digital sig-
nals. Digital sound and images are manipulated using the methods of DSP.

1. Complex Numbers

The basic manipulations of complex numbers are reviewed in this section. The
algebraic rules for combining complex numbers are reviewed.

1.1. Introduction. A complex number system is an extension of the real number
system. Complex numbers are necessary to solve equations such as

The symbol i is introduced to stand for 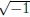, so the previous equation (1.1) has
two solutions z =± i . More generally, complex numbers are needed to solve for
the two roots of a quadratic equation

which, according to the quadratic formula, has the two solutions:

1.2. Notation for Complex Numbers. Several different mathematical nota-
tions can be used to represent complex numbers. The two basic types are polar
form and rectangular form. Converting between them quickly and easily is an
important skill.

1.2.1. Rectangular Form. In rectangular form, the following notations define the
same complex number z:

The ordered pair (x, y) can be interpreted as a point in the two-dimensional
plane. A complex number can also be drawn as a vector whose tail is located at
the origin and whose head is at the point (x, y), in which case x is the horizontal
coordinate of the vector and y the vertical coordinate. The complex number z =
2 +5i is represented by the point (2, 5), which lies in the first quadrant. Likewise,
z = 4− 3i lies in the fourth quadrant at the location (4, 3).

1.2.2. Polar Form. In polar form, the vector is defined by its length  (r) and its
direction ( θ ). The following descriptive notation is often used:

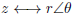
1.2.3. Conversion: Rectangular and Polar. Both the polar and rectangular forms
are commonly used to represent complex numbers. Given z = r∠θ , the x and y
coordinates are given by the following equations

Therefore, a valid formula for z is

Theorem 1.1. The sum of two or more cosine signals each having the same fre-
quency, but having different amplitudes and phase shifts, can be expressed as a
single equivalent cosine signal

proof

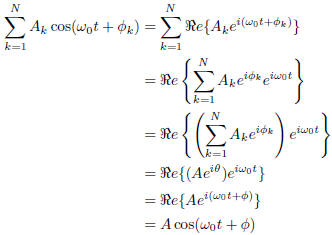
This completes the proof.

1.3. Sound Demo. Run the MATLAB sound demo by typing xpsound at the
MATLAB prompt. To generate a tone in MATLAB type in the following code:

1.4. Phasor Demo. The process of phasor addition can be accomplished easily
using MATLAB. The function zprint was used to create the following output.

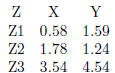
2. The Mandelbrot Set

2.1. Introduction. The Mandelbrot set is a subset of the parameter plane for
iteration of the complex quadratic function . Here the parameter
c is complex. The Mandelbrot set consists of those c values for which the orbit of
0 is bounded.