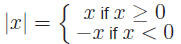- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Archimedean Property and Distribution of Q in R
1.2 Archimedean Property and Distribution of Q in R
Definition: We say the set S is dense in R if for
every a < b the intersection
S ∩ (a, b) ≠ Ø. (In other words, there is an element of S between every
two elements of
R.)
• The main goal of Section 1.2 is to show that the rationals are dense in the
reals. To achieve
this goal, the book first proves The Archimedean Property.
| Theorem 1.5 The Archimedean Property: For
any positive number c there is a natural number n in N such that n > c. (Equivalently, for any positive number ε, there is a natural number n such that 1/n < ε .) |
• Proof: That the two versions are equivalent is as simple
as noting that when ε = 1/c then
the same n works for both. However, we must now prove one of the two versions of
the claim.
Note that the first version is the same as saying N is not bounded. We will
assume that it has
an upper-bound and reach a contradiction. If it is bounded above, then the
completeness
axiom tells us that b = sup is a number in R with the property that n < b
for every
natural number n. But then, since n + 1 is also a natural number, we know n + 1
< b.
This is the same as n < b − 1 for every n, which means that b − 1 is an
upper-bound for
N, which contradicts the minimality of b.
• The next thing the book proves is a fact that may seem completely obvious to
us: “Theorem
1.8 For any number c, there is exactly one integer k in the interval [c, c +
1).” Note that it
takes about two pages to prove this result! Merely for the sake of time, we will
accept this
fact here without discussing the proof, but you should look at the proof if only
to see that it
can be proved using the axioms explicitly.
• Now, we will use the previous two results to prove the denseness of the
rationals:
| Theorem 1.9: If a and b are real numbers such that a < b then Q ∩ (a, b) ≠ Ø. |
• Proof: We need to find m, n ∈ Z such that
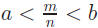 . We use Theorem 1.5 to get n
. We use Theorem 1.5 to get n
with 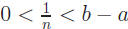 . By theorem 1.8 there is an integer m
in [nb − 1, nb). Thus:
. By theorem 1.8 there is an integer m
in [nb − 1, nb). Thus:
nb − 1 ≤ m <nb
b − 1/n ≤m/n < b (dividing by n)
a <m/n< b because a = b − (b − a) < b − 1/n.
• Similarly, we can show that the irrationals are dense in
R. This takes two steps...can we do
them together?
 Show that the product of an irrational
number and a rational number is irrational.
Show that the product of an irrational
number and a rational number is irrational.
 Show that there is an irrational number in
(a, b) by using the fact that there is a rational
Show that there is an irrational number in
(a, b) by using the fact that there is a rational
number in 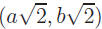
1.3 Inequalities and Identities
• This section contains a number of formulas that will
prove useful. Most important for us will
be:
| Theorem 1.11 Triangle Inequality:
|
• Proof: Since |c| ≤ d is equivalent to −d ≤ c ≤ d,
we can add together the formulas
−|a| ≤ a ≤ |a| and −|b| ≤ b ≤ |b| to get this.
• Why is it called the “triangle” inequality?
• Other formulas and definitions here should be equally familiar to you from
other classes, such
as:

and
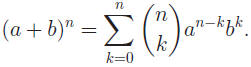
| Homework: 1.2 # 1 / 1.3 # 7 |



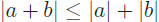 where
where