Maximizing Triangle Area

Following is the problem we worked on early this year in Precalculus:

Take a sheet of paper and fold the
upper left corner so that it touches
some point on the bottom edge, as
illustrated here. Consider the area of
the triangle labeled “A” – the one
formed in the lower left corner of the
paper. Find the dimensions of the
triangle that has the largest area.


Students worked in groups to collect data; each group had different-sized sheet of paper.
Expectations included a written report that included both a “data solution” and an “algebraic
solution.” This talk looks at those solutions, plus extensions involving more data analysis and
calculus.

Let’s begin with a sample data set collected from folding an 8.5” x 11” sheet of paper:


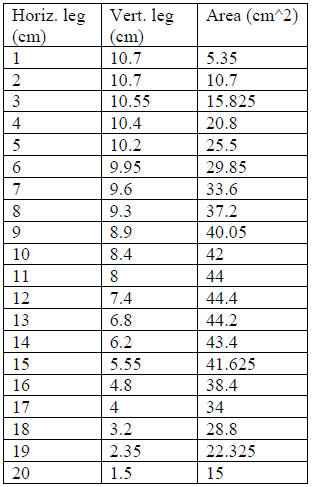
And some plots of our data:

Area (cm^2) vs. Horiz Leg (cm)


Area (cm^2)


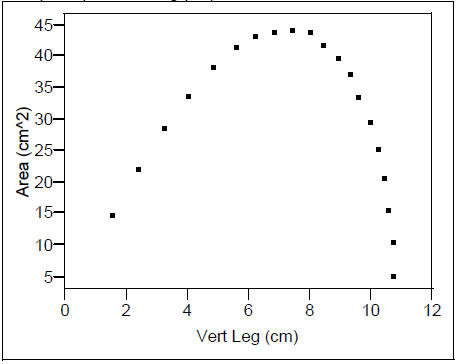
By inspecting our data and scatterplot, we see the maximum area is approximately 44.4 cm^2,
when the dimensions are approximately 12 cm x 7.4 cm.

What functions best describe the relationships in the scatterplots above? Quadratic? Some other
polynomial? Something else? (Will revisit this question soon…)

Or, can we predict the vertical leg length if we know the horizontal leg length?

Vert Leg (cm) vs. Horiz Leg (cm)


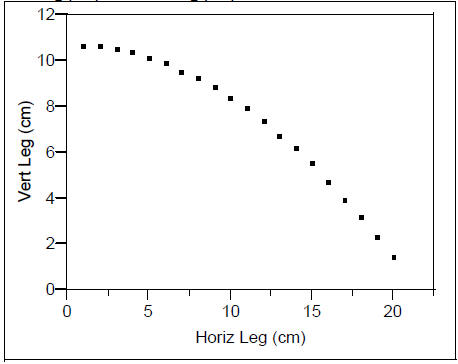
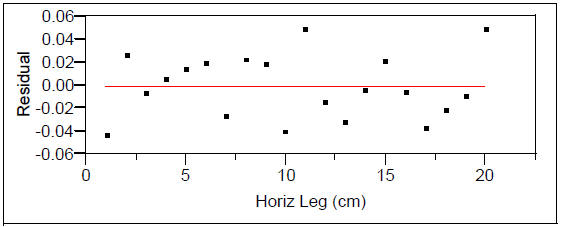
Seems to be parabolic? (The quadratic fit on the next page seems promising – the residuals show
no obvious pattern!)

Bivariate Fit of Vert Leg (cm) By Horiz Leg (cm)
Polynomial Fit Degree=2
Vert Leg (cm) = 10.7646 - 0.000571 Horiz Leg (cm) - 0.023314 (Horiz Leg (cm))^2

So, we could write 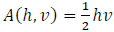, and with 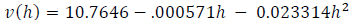, we
have 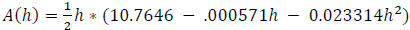. (Where 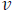and 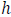are the vertical
and horizontal legs of the triangle, respectively.) Then if we graph this function, we notice it
matches our “area vs horiz. leg” scatterplot well and we can use our calculator to find the
maximum area of 44.56 cm^2, with a horiz. leg length of 12.4 cm. Then 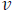(12.4)= 7.18 cm
would be the vertical leg length.

What about domain?

Notice that our model A(h) (as given above) is a cubic polynomial. Polynomials have domains
of all real numbers, but is this a sensible domain in the context of our problem? It would only
make sense to have A(h)> 0, and a quick inspection reveals that for this to be the case, we must
have 0 <h< 21.5 (approximately). (Why 21.5? Notice this is approximately the shorter
dimension of the sheet of paper.)

Algebraic Approach

Realizing that the hypotenuse of our right triangle is simply the difference between the shorter
side of the sheet of paper and the triangle’s vertical leg, we can label our figure as such:


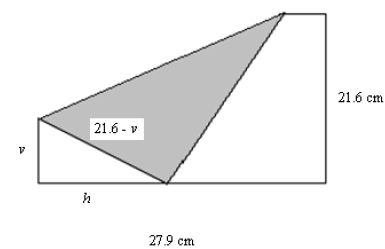
Then starting with Pythagorean Theorem, we have


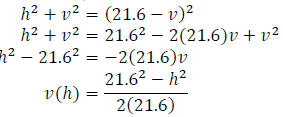
Then, since 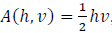, we have


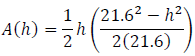
Notice that in order to have A(h)> 0 we need 0 <h<  21.6.
Graphing this function in our calculator, we find the maximum area of 44.9 cm^2, when the
horizontal leg is 12.47 cm.

What if we had chosen to write our model for area in terms of the vertical leg instead?
Then we would write 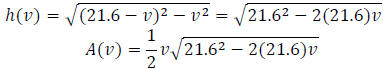,and
Of course we still find the same maximum area of 44.9 cm^2, but with a vertical leg length of
7.2 cm. Notice that while A(h) is simply a cubic function, A(v) is not even a polynomial;
perhaps something different than what Precalculus students may be used to, and thus explaining
the slightly different shapes of our earlier scatterplots of A(h) and A(v). (Notice for A(v), the
“domain of reality is 0 <v< 21.6/2.

An Extension

What if we used a different-sized sheet of paper?
Redo the activity with various sizes of paper and collect data on the dimensions that maximize
the triangle’s area. Some sample data follows:



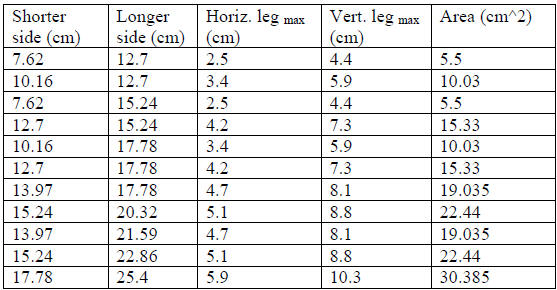
Can we predict the horizontal leg length that maximizes the area from one of the side lengths of
the paper?

Horiz Leg_max (cm) vs. Shorter Dimension (cm)


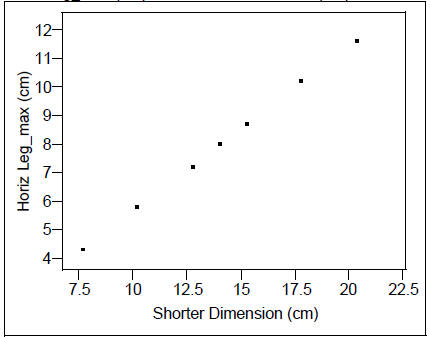
Seems linear; let’s try a linear fit and check the residuals:

Linear Fit
Horiz Leg_max (cm) = 0.0257143 + 0.575928 Shorter Dimension (cm)


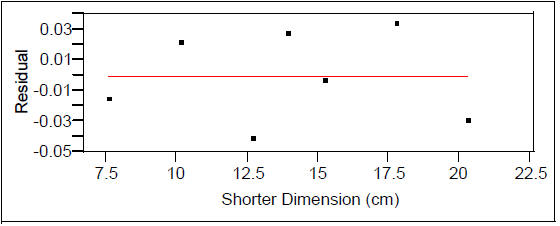
Looks good; what if we had tried to predict the horizontal leg length that maximizes the area
from the longer dimension?

Horiz Leg_max (cm)


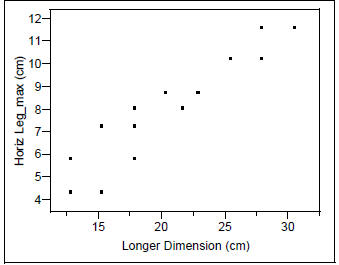
While there seems to be some relationship; it’s not as clearly defined as the relationship between
the Horiz. Leg length and the shorter dimension.

So if h (x)=0.0257143 + 0.575928s (where h is the horizontal leg length that maximizes the
area and s is the length of the shorter dimension of the paper) is a good model to predict the
horizontal leg length, could we also model the vertical leg length from the shorter-side
dimension?

Vert Leg_max (cm) vs. Shorter Dimension (cm)


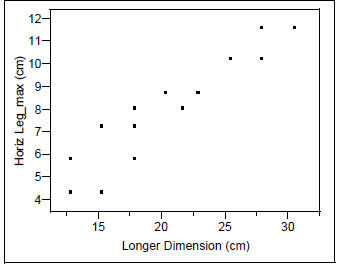
Looks linear based on the scatterplot; residuals confirm a good fit:

Linear Fit
Vert Leg_max (cm) = -0.041429 + 0.336333 Shorter Dimension (cm)


So, we seem to be able to predict the vertical leg length by v(s) = -0.041429 + 0.336333s,
where v is the vertical leg length that maximizes area and s is the length of the shorter dimension
of the paper.

Possible extension:
While the linear models for h(s) and v(s) seem very reasonable; it would perhaps be
advantageous for h(s) and v(s) to be “forced” to pass through (0,0), since a shorter-side
dimension of 0 cm would necessarily imply triangle legs of length 0. Then our models become
h(s)= 0.5776282s and v(s)= .3335938 with the following residual plots: (See Appendix 2
for a formula for this regression method.)

Horiz Leg_max (cm) vs. Shorter Dimension (cm)

Linear Fit
Horiz Leg_max (cm) = 0 + 0.5776282 Shorter Dimension (cm)


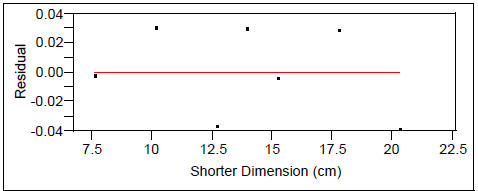
Vert Leg_max (cm) vs. Shorter Dimension (cm)

Linear Fit
Vert Leg_max (cm) = 0 + 0.3335938 Shorter Dimension (cm)


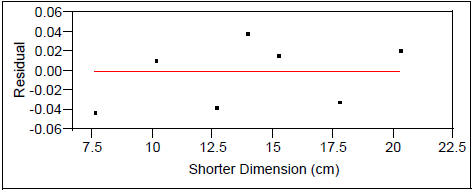
Finally, what if we try to predict the maximum area from the shorter paper dimension?

Max Area (cm^2) vs. Shorter Dimension (cm)


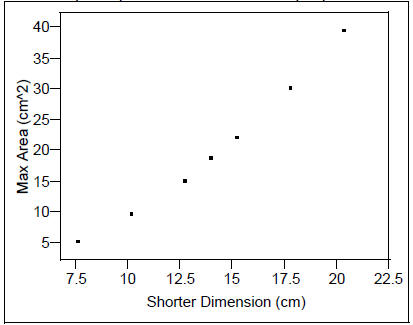
Could a linear model be a good fit? Not when we look at superimposed least-squares line and the
residual plot:

Max Area (cm^2) vs. Shorter Dimension (cm)


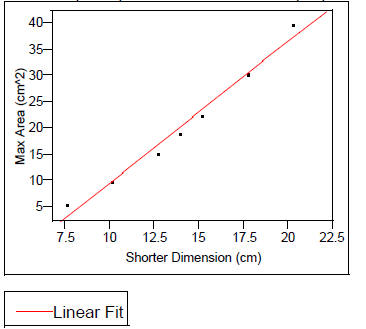
Linear Fit
Max Area (cm^2) = -17.29036 + 2.6948819 Shorter Dimension (cm)


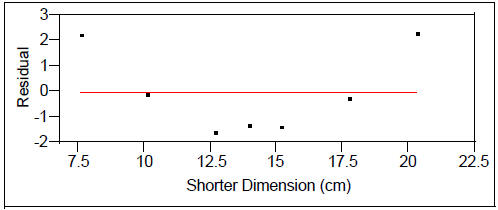
Besides, if each leg is well-modeled by a linear function of the shorter dimension, then it seems
reasonable that the area should be modeled by a quadratic function of the shorter dimension:

Max Area (cm^2) vs. Shorter Dimension (cm)


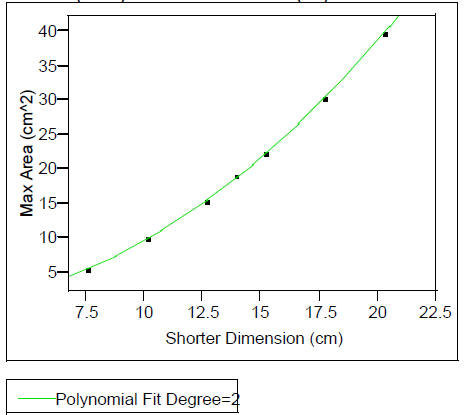
Polynomial Fit Degree=2
Max Area (cm^2) = -18.81004 + 2.6948819 Shorter Dimension (cm) + 0.0942202 (Shorter Dimension (cm)-13.97)^2


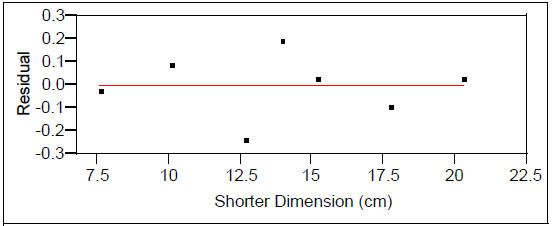
Alternately, we could use re-expression to find a model for the area as a function of shorter
dimension. Since we think quadratic is a good model, we can take the square root of the area:

sqrt(max area) vs. Shorter Dimension (cm)


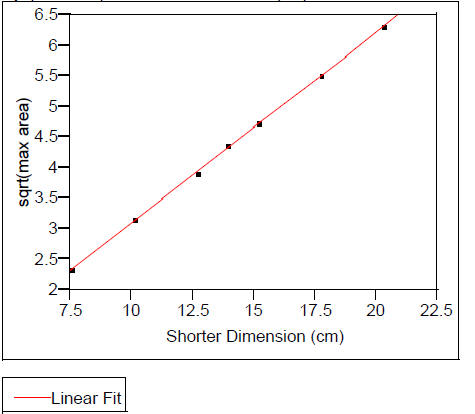
Linear Fit
sqrt(max area) = -0.012407 + 0.3112161 Shorter Dimension (cm)


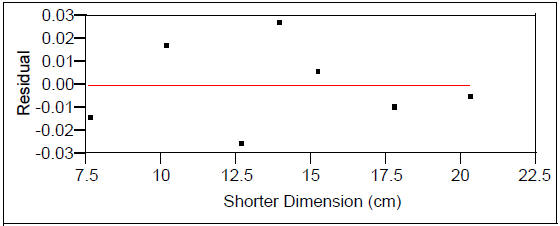
When we write our model back in terms of the maximum area, we have:


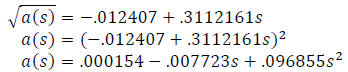
(where a(s) is the maximum triangle area for a sheet of paper with shorter dimension s).

Again, as a possible extension, we might “force” our linear model through the origin (since it
makes sense that a shorter dimension of 0 cm would imply an area of 0). Then our model would
be:

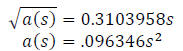
Calculus method

Earlier we had


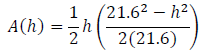
as a model to predict the area, A, as a function of horizontal leg length, h. Noticing that the
“21.6” is simply the shorter dimension of the sheet of paper (in cm), we can make our solution
more general by writing


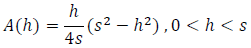
where s is the shorter dimension of the sheet of paper. (Notice that, as we observed earlier, the
maximum area is dependent only on the shorter dimension of the sheet of paper, not the longer
dimension.)
Then we can find the value of h that maximizes A as follows:


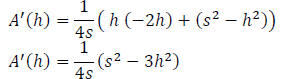
Setting 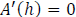we have 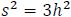, so 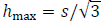. (An easy check with the 2nd derivative
test verifies it is indeed a maximum.)

Alternately, if we had chosen to work with

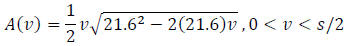
instead, the algebra is slightly more challenging:


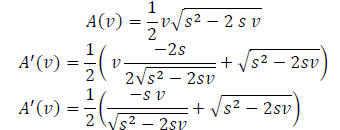
Then setting we have


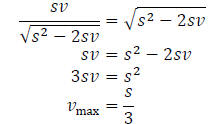
Since and 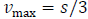, it therefore follows that

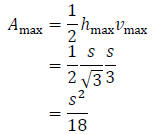
Appendix 1

Excerpts from a sample student handout:
Triangle Problem Writing Assignment

o Write alone, but you may consult with others in your group.

o Characteristics of your paper:
o It should be “self-contained”, meaning that you could mail it to a friend back home
who knows the math you know, and s/he would be able to follow your thinking.
o You can do it all by hand, or type the words and do the rest by hand, or learn
MathType and do the equations in a Word doc also.
o Include your name and the names of your pod-partners, a signature (which indicates
that you were academically honest in doing this work), the name of the assignment,
the date handed in, and your class block’s letter.

o The paper should contain:
o A description of the problem. (If you decide to take the description of the problem
word-for-word from the handout, you must cite the source.)

o The “data solution”, which should include (with words wrapped around them, of
course):
The actual data, including units
A scatter plot (with axes labeled with words and a scale)
An answer, as an ordered pair and in words

o The “algebra solution”, which should include:
Identifying your variables
The work leading up to your model
The model
A sketch of the model over the domain of reality (and why that is the D.of.R)
An answer, as an ordered pair and in words

o A comparison of the two answers

If you want to say more (like, what you got by punching “magic buttons”, or looking at the
relationship between base and height of the triangles), feel free

Appendix 2

Linear Regression with a “forced” intercept at 0.
The goal of regression is to minimize the sum of the squares of the residuals. We start with
ordered pairs and the linear model y=mx.


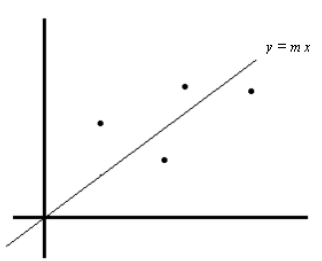
Since a residual is “actual y” – “predicted y,” each residual can be written as 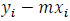. So we set
out to minimize the sum of the squares of the residuals, or


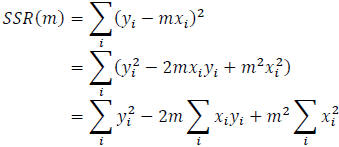
To find the value of a that minimizes SSR(m), we take the derivative with respect to m:

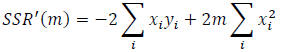
Setting the derivative equal to zero, we have

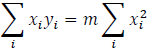
therefore

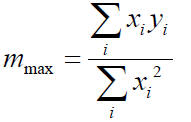
gives the slope of the line through the origin that minimizes the sum of the squares of the
residuals.