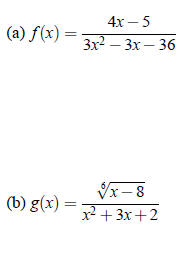Math 142 - Chapter 2 Lecture Notes

The purpose of this handout is to facilitate your note-taking during lecture. This handout is not a comprehensive summary of the chapter; I will be giving additional notes during lecture which you will also be responsible
to know for exams and quizzes. Some of these examples come from examples and exercises in Calculus for Business, Economics, Life Sciences, and Social Sciences, 11th ed. by Barnett, Ziegler, and Byleen.

Section 2.1 - Functions

Function -

Domain - The set of _______ of a function; i.e., the set of values for which it makes sense to plug into the function.

Range - The set of _______ of a function; i.e., the set of values obtained by substituting all input values into the
function.

NOTE: When graphing a function, x represents ____________________________and y represents ____________________________

Functions Specified by Equations
The correspondence between domain and range elements is often specified by an equation in two variables. For example,
consider y = 3x+7. In equations like these, we refer to x as ____________________________ the (since values
can be ____________________________ from the domain), and we refer to y as the____________________________
____________________________(since the value of y____________________________

If in an equation in two variables, we get exactly one output (value for the dependent variable) for each input (value for
the independent variable), then the equation specifies a function.

Example 1 - Determining Algebraically Whether an Equation Specifies a Function
Determine which of the following equations specify functions with independent variable x. (Assume x represents a real
number in each equation.)

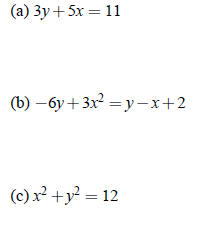
Identifying Functions - Vertical Line Test
Suppose that a graph has inputs located on the x-axis and outputs located on the y-axis. If at any input you can draw a
vertical line that crosses the graph in two or more places,____________________________

Example 2 - Identifying Functions
Which of the following graphs are functions?

NOTE: If a function is specified by an equation and the domain is not indicated, then we will assume that the domain
is the set of all real numbers that, when substituted for the independent variable, produce real output values for the
dependent variable.

Example 3 - Warm-up: Finding Domains
Find the domain of each of the following functions, assuming that x is the independent variable.

Finding Domains
The domain of a function is all real numbers unless

• the function involves a ____________________________. In this case, exclude____________________________

• the function involves an ____________________________. In this case, exclude____________________________

• the function involves a ____________________________. In this case, exclude____________________________

• the function represents a ____________________________. In this case, the domain should be restricted to____________________________

Example 4
Find the domain of each of the following functions, assuming that x is the independent variable.

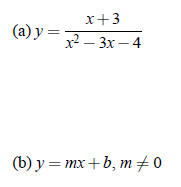
NOTE: The vertical line test implies that equations of the form y=mx+b, where m≠0, specify functions; they are called ____________________________. Similarly, equations of the form y=b specify what are called ____________________________

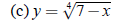
Function Notation
It is often useful to assign names to functions using letters. For example, if f denotes the function specified by the
equation y = 3x^3 −9, then we can write __________________________. We use the symbol __________________________in place of y to designate the output value in the range that is obtained when the input value x is substituted into the function.

Example 5

Let f(x) = x^2 −2x+1 and 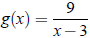Find each of the following.

Difference Quotient

The expression 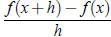, where x and x+h are in the domain of f and h ≠ 0, is referred to as the difference
quotient and is studied extensively in calculus.

Example 6
Find the difference quotient for f (x) = x^2−4x+1 by finding each of the following.

Applications: Break-Even and Profit-Loss Analysis

• Cost function
• Price-Demand Function
• Revenue Function
• Profit Function

• A company will have a loss if __________, will break even if __________, and will have a profit if__________

Example 7
Acme Computer Company has a variable production cost per computer of $180, and has fixed costs that amount to
$45,000. Acme’s sales research department has established the price-demand function for its computers to be p =
−0.23x+574 dollars per computer. Using this information, find each of the following.

(a) Cost Function

 

(b) Revenue Function

 

(c) Profit Function

 

(d) Graph these three functions on the same coordinate axes. What do you notice?

 

Section 2.2 - Elementary Functions and Piecewise Functions

Elementary Functions

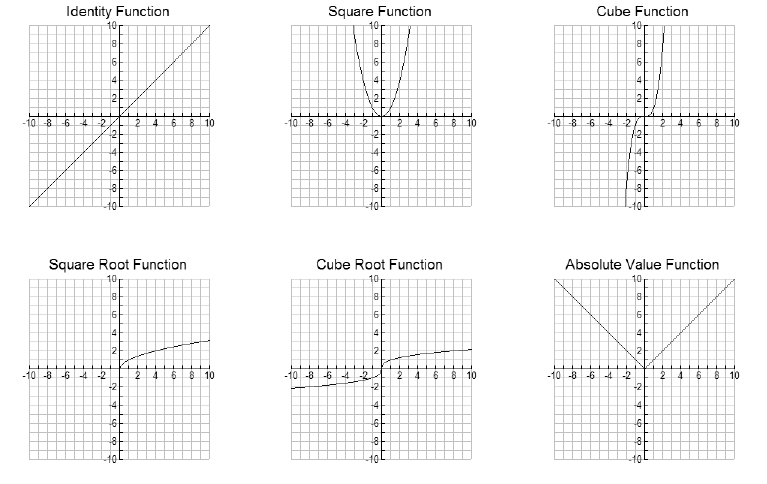
Graph Transformations of y = f (x)

1. Vertical Translation

• If y = f (x)+k, shift the graph of y = f (x) _____________________ if k > 0 and  _____________________ if
k < 0.

2. Horizontal Translation

• If y = f (x+h), shift the graph of y = f (x) _____________________ if h > 0 and _____________________ if
h < 0.

3. Reflection

• If y = −f (x), reflect the graph of y = f (x) _____________________.

4. Vertical Stretch and Shrink

• If y = A f (x) where A > 1, stretch the graph of y = f (x) vertically by multiplying each y coordinate value by
A.
• If y = A f (x) where 0 < A < 1, shrink the graph of y = f (x) vertically by multiplying each y coordinate value
by A.

Example 1
Sketch the graph of g(x) = − | x+3 | +4.

Example 2 Suppose that we are given the graph of a function f . How must we transform the graph of f to obtain the
graph of g if g(x) = 6−4 f (x−3)?

Definition: A function whose definition involves different rules for different parts of its domain is called a_____________________

Recall: The absolute value function:

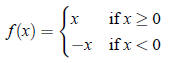
Example 6

Consider the function

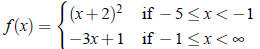
(a) Find f (−2), f (−1), and f (10).

 

(b) Sketch the graph of f .

 

Example 7
AB&C’s monthly cell phone service charges are as follows: All customers pay a flat rate of $35 per month, and then
additional charges are added based on the number of minutes of air time used. The first 100 minutes are free, but for the
next 100 minutes, a fee of $0.05 per minute is added. Any minutes used beyond this are charged at a rate of $0.15 per
minute. Let x represent the number of minutes of air time used by a customer in one month.

(a) Write a function f in terms of x that gives a customer’s monthly bill.

 

(b) Find and interpret f (75), f (150), and f (400).

 

(c) Sketch the graph of f .

 

Read Example 6 and Matched Problem 6 on pages 70 and 71.
Suggested Homework: 1-17 odd, 23, 25, 29-41 odd, 43-48 (all), 65-68 (all)

Section 2.3 - Quadratic Functions

Quadratic Function
If a, b, and c are real numbers with a ≠ 0, then the function _____________________ is a quadratic function.

Finding Intercepts of a Quadratic Function

• To find the y-intercept of a quadratic function f , calculate_____________________

• To find the x-intercept(s) (if any exist) of a quadratic function f , you have three options:

1.
2.
3.

Example 1
Find the x and y-intercepts of the following quadratic functions.

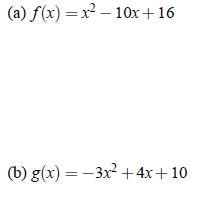
Examples: Graphs of Quadratic Functions

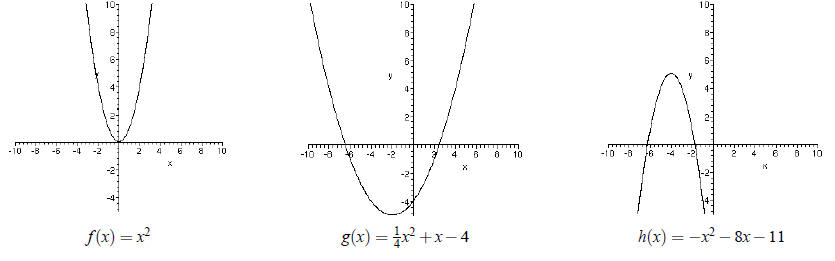
Properties of the Graph of a Quadratic Function y = ax^2 +bx+c

• The graph of a quadratic function is a _____________________.
• The lowest or highest point on the _____________________, whichever exists, is called the _____________________.
• If a>0, then the parabola opens _____________________, and the _____________________ value of the quadratic function
occurs at the vertex.
• If a<0, then the parabola opens _____________________, and the_____________________ value of the quadratic function
occurs at the vertex.
• The vertical line passing through the vertex of a parabola is called the _____________________ of
the parabola, or simply the _____________________ .

Example 2
Use graph transformations to graph f (x) = −(x−2)^2+3

Example 3
Find the vertex, axis of symmetry, maximum or minimum value (whichever exists), x and y intercepts, domain, and range
of the quadratic function given in Example 1.

NOTE: Carefully examine the vertex you found in Example 3 for the function f (x) = −(x−2)^2+3. Notice anything?

The Vertex Form of a Quadratic Function
Using a process called _____________________, a quadratic function f (x)=ax^2+bx+c can be rewritten
into the form

which is called the vertex form of a quadratic function. When a quadratic function is written in the vertex form, we have
the following general properties:

1. The vertex of the parabola is _______________ . (Note k = ________ )
2. The axis of symmetry is the vertical line _______________ .
3. f (h) = k is the _______________  if a > 0 and the _______________  if a < 0.
4. The domain of a quadratic function is _______________ .
5. The range of a quadratic function is _______________  if a > 0 or _______________  if a < 0.

Another Method for Finding the Vertex of a Parabola
It can be shown using the method of completing the square that, given a quadratic function f (x) = ax^2 +bx+c,

• the x coordinate of the vertex (h,k) is given by _______________ .
• the y coordinate of the vertex (h,k) is given by _______________ .
• If a > 0, then the _______________  value of f occurs at 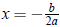and has value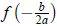
• If a < 0, then the _______________  value of f occurs at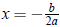and has value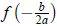

Example 4
Find the minumum value of g(x) = 5x^2 −7x+2.

Example 5 (adaptation of #58, pg. 92 of Barnett, Ziegler, and Byleen)
The market research department for a company that manufactures widgets established the price-demand function to be
p(x) = 2000−60x, where p(x) is the wholesale price per widget in dollars at which x widgets can be sold. This company
has fixed costs that amount to $4,000, and the variable production cost per widget is $500.

(a) Find this company’s break-even point(s).

(b) Find the output that will produce the maximum revenue, and find the maximum revenue.

(c) Find the maximum profit.

(d) What price should the company charge per widget to achieve maximum profit?

Polynomial Functions
A polynomial function is a function that can be written in the form

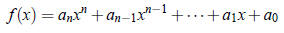
where n is a nonnegative integer called the  _______________ of the polynomial. The coefficients a₀,a₁, . . . ,a_n are real
numbers with a_n ≠ 0 (a_n is called the  _______________). The domain of a polynomial is _______________

Examples of Polynomials, Degree 1 through Degree 6, a_n > 0

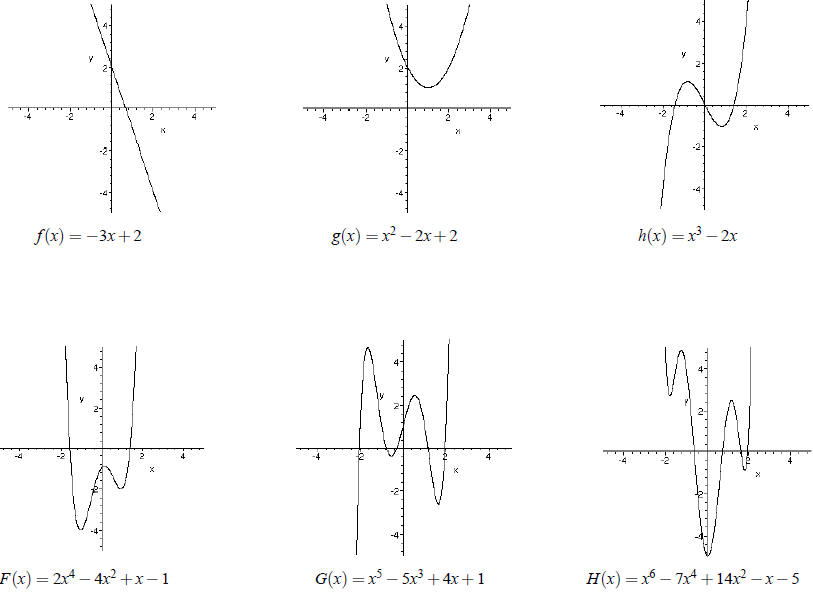
Properties of Polynomials

• For even-degree polynomials, both “ends” of the graph will go to if the leading coefficient is positive, and both
“ends” of the graph will go to if the leading coefficient is negative.
• For odd-degree polynomials, the graph starts negative and ends positive if the leading coefficient is positive, or the
graph starts positive and ends negative if the leading coefficient is negative.
• An odd-degree polynomial will cross the x-axis at least once.
• An even-degree polynomial may never cross the x-axis.
• In general, a polynomial of degree n can have at most n linear factors. Therefore, the graph of a polynomial of
positive degree n may intersect the x axis at most n times.
• The graph of a polynomial is continuous. That is, the graph can be drawn without removing a pen from the paper.
• The graph of a polynomial is smooth. That is, the graph has no sharp corners.

Rational Functions
A rational function is any function that can be written in the form

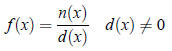
where n(x) and d(x) are polynomials. The domain is the set of all real numbers such that _______________

Examples of Rational Functions

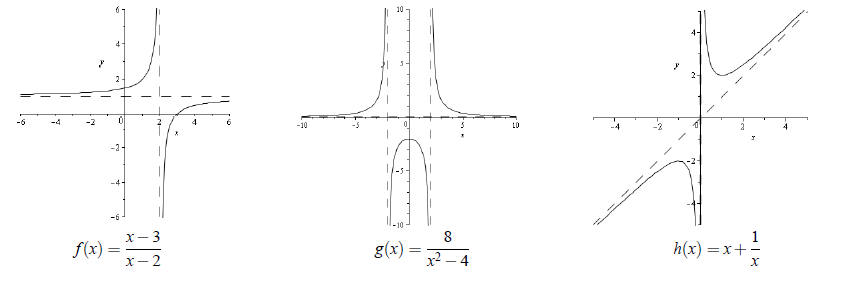
Example 6
Find the domain of each of the following and state whether or not each is a rational function.