- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Survey of Algebra
COURSE GOALS:
Survey of Algebra is the second algebra course we offer (and would be better
named
“Intermediate Algebra”). This course is also the prerequisite class for most of
the college level
transfer classes we teach (MAT 120 “Math for Liberal Arts”, MAT 121 “College
Algebra”, and
MAT 123 “Finite Math”, MAT 135 “Statistics”, and MAT 155/156 Integrated Math
I/II “Math
for Elementary Teachers”). Note that MAT 106 is not a prerequisite for MAT 107
“Career
Math”. 22 of the 38 sections covered in MAT 106 are a review from MAT
090! This is
intentional.
Most students will take MAT 121 (College Algebra) after this course. In light of
that, students
need to get a strong foundation in algebraic skills in this course, and end of
the semester grades
should be with the notion that students need to be prepared for MAT 121.
Since there are so many options after 106, we want to give students (or at least
discuss with
them) the Life After MAT 106 handout about other class choices. This
discussion should take
place near the registration period. This allows students to register for the
correct class initially
rather than arrive in 121, discover they could take another class, and have to
rearrange their
schedule. Some 106 instructors have even made an assignment where students
obtain (in writing
or off a web page), the math class they need for their FR degree or transfer
institution.
GUIDING PRINCIPLES:
The following principles are intended to create the “framework for success” that
our students
need in order to become confident and competent learners.
1. Memorizing is the lowest form of learning on Bloom’s Taxonomy. Memorizing
basic
algebraic procedures is key to a strong foundation in College Algebra. For
example,
students need to be able use the laws of exponents.
COURSE SUGGESTION: The use of note cards, class notes, or the textbook for an
exam
is discouraged. The reason for this is to facilitate the memorization of basics
of algebraic
procedures (i.e. factoring) and formulas and to motivate serious study. If note
cards are
to be used, restrictions should be placed on what type of information can be
placed on it.
2. At this level, it is important to keep students awake, alert, and engaged.
COURSE SUGGESTION: Make sure to give breaks. Have you heard this: “The brain
can only absorb as much as the tush can endure.” Most MAT 106 classes are twice
a
week for 1 hour and 50 minutes. This time unit has a 10 minute break built into
it. The
more the students sit and watch, the less their brain is engaged. It is better
for students to
have this break half way through the class, versus being let out 10 minutes
early. A break
allows the students to get up and get their blood pumping again. Breaks are even
more
crucial to the Saturday morning classes.
COURSE SUGGESTION: Engaging students is critical. Students
not only need to see
how problems are done, they need to try some of the problems during class. A
format
that works well with this level of student is to teach for a few minutes, and
then problems
for students to work on for a few minutes. If your lecture is over before class
is over,
have students start trying to work homework problems, while you are still there
to help.
3. In this foundational algebra course, it is important to emphasize good
algebra habits.
COURSE SUGGESTION: It is important to emphasize proper vocabulary in the course.
For example, many students know to take the square root of both sides of x2 = 49
yet say
“square both sides” when asked what step to do next.
.
COURSE SUGGESTION: The Dugopolski text has excellent Reading and Writing
exercises (usually the first few of each exercise set), called “Enriching your
mathematical
word power”. It helps reinforce vocabulary and notation.
COURSE SUGGESTION: Besides the course content, it is important to emphasize the
difference between an expression and an equation, and what you can do with each.
COURSE SUGGESTION: Emphasize that 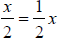 and
and
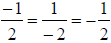
4. Assessment of achievement should be taken seriously. We
want grades to reflect student
achievement (see #5).
COURSE SUGGESTION: It is important to know who is taking the exams. Exclusive
use of take-home assessments is not allowed. Also, the in-class final exam needs
to be
cumulative so that students have one last opportunity to “pull it all together”!
5. Grade on achievement. Grading on attitude, effort, behavior, or a student’s
“need” for a
certain grade does a disservice to the student, to the student’s subsequent
instructor, and
to Front Range Community College.
COURSE SUGGESTION: Remember, we are teaching more than math!!!! Sometimes
the lessons involve responsibility. Just because a student earns a low grade,
does not
mean they did not learn anything.
GATEWAY TOPICS (if applicable): Currently not applicable for MAT 106.
| See Course Specifics for details about current book, coverage, and technology issues. |
CURRENT TEXTBOOK:
Intermediate Algebra, 5th Edition, by Mark Dugopolski.
CONTENT:
22 of the 38 sections covered in MAT 106 are a review. The following sections
are required.
See notes below about specific sections.
• All of chapter 2
• All of chapter 3
• 4.1 – 4.3 (only briefly on 4.3)
• All of chapter 5
• All of chapter 6
• All of chapter 7
• 8.1, 8.2, 8.4
Below is a possible schedule, broken down in 30 days of class. Adjust
accordingly.
® means this is a review section, so in theory, you can cover it more quickly.
| Day | Cover | Notes |
| 1 | Intro to course, 2.1® , 2.2®, | |
| 2 | 2.3®, 2.4® | |
| 3 | 2.5®, 2.6 | |
| 4 | Review | |
| 5 | Exam (Chapter 2) | hopefully this is before drop date |
| 6 | 3.1®, 3.2®, 3.3 | Skip midpoint and distance formula in 3.1 |
| 7 | 3.4, 3.5 | Skip 61-76 in 3.4 (Absolute Value Inequalities) |
| 8 | 4.1, 4.2, 4.3 | Only briefly cover 4.3 |
| 9 | Review | |
| 10 | Exam (Chapters 3 and 4) | |
| 11 | 5.1®, 5.2®, 5.3® | |
| 12 | 5.4®, 5.5® 5.6® | In 5.5, sum & diff of cubes is NEW! |
| 13 | 5.7®, 5.8® | |
| 14 | Review | |
| 15 | Exam (Chapters 5) | |
| 16 | 6.1®, 6.2®, 6.3® | |
| 17 | 6.4®, 6.5® | Emphasize complex fractions (it’s a review, but
students probably didn’t get it the first time). Skip synthetic division |
| 18 | 6.6®, 6.7® | |
| 19 | Exam (Chapter 6) | |
| 20 | 7.1, 7.2 | |
| 21 | 7.3, 7.4 | |
| 22 | 7.5, 7.6 | |
| 23 | Review | |
| 24 | Exam (Chapter 7) | |
| 25 | 8.1, 8.2 | Leave out 8.2 #31-46 (discriminants) |
| 26 | 8.4 | Emphasize equations reducible to quadratic #33-80 |
| 27 | Review | |
| 28 | Exam (Chapter 8) | |
| 29 | Review | |
| 30 | Cumulative Final |
TECHNOLOGY:
MATHZONE is a web-based supplement that is specific
to our
textbook. It has unlimited number of exercises for practice; free access to live
online tutoring via
NetTutor; e-Professor, animated step-by-step instruction for solving problems in
the book; textspecific
lecture videos; and self-tests.
Calculators: The use of graphing calculators in 106 should be restricted so that
students learn
graphing basics by hand. It is up to the instructor whether or not to require a
calculator. Since
the graphing calculator rental program is reserved for college level courses
(those above 106), if
any type of calculator is required in 106, one may want to consider using
scientific calculators. I
personally don’t allow any calculators on my 106 exams.
Video Tapes & CD Lecture Series: Available at the Math Lab. The Media Center
will also
have a copy of the video tapes which can be checked out and viewed on site. Some
students find
it very helpful to see the lectures more than once. The video tapes are a great
way to do that.
The videos are also available on MathZone.
NOTES ABOUT CURRENT TEXT: None
SUPPLEMENTS:
• “Life After 106” handout
Specific Things that Should be Emphasizes by Chapter:
Thoughts from Monica and Ryan
A Work in Progress. Looking for input from 106 and 121 instructors.
CHAPTER ANALYSIS:
Chapter 2: Linear Equations and Inequalities in One Variable
• Calculator Comments
o Only allow scientific calculators
• Section 2.4
o Interval Notation
• Section 2.6
o Point out that the absolute value definition is piecewise.
Chapter 3: Linear Equations and Inequalities in Two Variables
• Calculator Comments
o Only allow scientific calculators
• Sections 3.1-3.5
o Being able to graph functions using a T table (plotting
points)
o Function notation f(x) does not mean “f times x”
o Students need to have strong foundation in functions (linear). They need to
have
strong graphing skills, as well as graph reading skills.
o Graph Reading
a. Evaluate the function at an x-value, i.e. f(3)=
b. Determine x when f(x) is given, i.e. When f(x) = 3, x =
c. Write the domain using interval notation
d. Write the range using interval notation
e. Write the x-intercepts using ordered pairs
f. Write the y-intercept using ordered pairs
g. Determine the slope of a line
h. Determine points of discontinuity, i.e. x = 3
Chapter 4: Systems of Linear Equations
• Calculator Comments
o Only allow scientific calculators
o Solve these systems by hand ! ☺
• Sections 4.1-4.3
o Word problems: especially setting up and defining the variables.
Chapter 5: Exponents and Polynomails
• Calculator Comments
o NO calculator at all – in order to help reinforce operations of signed numbers
• Sections 5.1 – 5.2
o Rules of exponents should be memorized.
Chapter 6: Rational Expressions and Functions
• Calculator Comments
o NO calculator at all – in order to help reinforce operations of signed numbers
Chapter 7: Radicals and Rational Expressions
• Calculator Comments
o NO calculator at all – in order to help reinforce operations of signed numbers
Chapter 8: Quadratic Equations, Functions, and Inequalities
• Calculator Comments
o NO calculator. Students need to be able simplify the quadratic formula. For
example, they need to be able to simplify 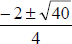 without a calculator. They
without a calculator. They
need to know 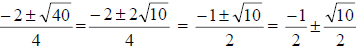 . This is a super
. This is a super
important skill – and should be done without a calculator. In fact, you may want
to emphasize this example in the quadratic formula section.
• Sections 8.1-8.2
o Completing the Square
o Quadratic Formula
 Quadratic Formula should be memorized. College Algebra teachers will
Quadratic Formula should be memorized. College Algebra teachers will
be expecting students to have it memorized!!! In fact, this is majorly
important…College Algebra students should ALREADY know
this!!!!!!!!!☺


