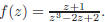- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Complex Numbers, Complex Functions and Contour Integrals
2. Complex Functions
Now that we’ve extended our collection of numbers to the
field of complex numbers, we can begin studying
complex-valued functions. The attempt to extend the theory of calculus to such
functions is the branch of
mathematics known as complex analysis. In the complex world, both
differentiation and integration gain new
depth and significance. As a sacrifice, however, we must severely limit the
class of functions we can analyze,
restricting to so-called analytic (or holomorphic) functions. For a rough
definition, suppose f(x, y) is any
complex-valued function of two real variables. Let z = x + iy. We call z the
complex variable. By Exercise 3,
we can use the identities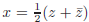 and
and
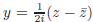 to express f(x, y) as a function of z and
to express f(x, y) as a function of z and
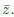 Morally,
Morally,
the function f is analytic if it does not depend on
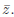 The analytic functions are exactly the
complex functions
The analytic functions are exactly the
complex functions
for which a derivative exists.
z^2 + 2iz + 3, we compute:
>> p=[1 2*i 3];
>> r=roots(p)
r =
0 - 3.0000i
0.0000 + 1.0000i
Thus, the roots are z = −3i and z = i.
Exercise 4. Find the roots of f(z) = z^4 − iz^3 + 2i.
It is a fact that all complex polynomials are analytic. We
can use polynomials to construct more general
complex functions. For instance, consider a quotient of two complex polynomials,
say f(z) = p(z)/q(z) . For simplicity,
assume p and q have distinct roots. It is then a fact that f is analytic away
from the roots of q, which we call
the poles of f. More generally, we have the following definition:
Definition. Suppose f is a function which is
analytic in a neighborhood of a point a, except perhaps at a itself.
If 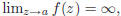 then the point a is said to be a pole of
f.
then the point a is said to be a pole of
f.
By the following fact, the nature of a general pole is exactly the same as in the case of a rational function:
Fact. If f has a pole at a, then there exists a
positive integer n and analytic function g not vanishing at a such
that
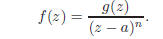
The integer n is called the order of the pole. Poles of order one are called
simple poles. A function which is
analytic away from a discrete set of poles is a called meromorphic. A function
which is analytic everywhere is
sometimes called entire.
By the previous example, we know the function
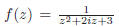 is a meromorphic function with simple
is a meromorphic function with simplepoles at z = −3i and z = i.
Exercise 5. What are the poles of
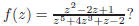
Associated to every pole of a meromorphic function f is a special number called the residue of f at that pole.
Definition. Suppose f is a meromorphic function
with a pole at a. The residue of f at a is the unique complex
number R such that
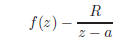
is the derivative of an analytic function in a
neighborhood of a, excluding a itself. We’ll usually denote this
number by 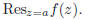 .
.
This definition may seem rather arbitrary, but in Section
3 we’ll see that residues are intimately linked with
integration.
Fortunately, MatLab can directly calculate residues of rational functions using the residue command. For
example, to compute the residues of
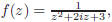 we
enter:
we
enter:>> p=[1];
>> q=[1 2*i 3];
>> [r, a, k]=residue(p,q)
r =
-0.0000 + 0.2500i
0.0000 - 0.2500i
a =
0 - 3.0000i
0.0000 + 1.0000i
k =
[]
MatLab has outputted the residues r at the
corresponding poles p. In this case, we see that
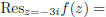
0.25i and 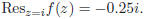
Exercise 6. Find the poles and corresponding
residues of the function