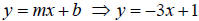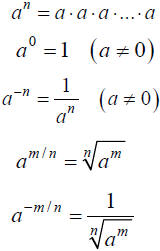Precalculus Review

• Precalculus Review I
• Precalculus Review II
• The Cartesian Coordinate System
• Straight Lines

The Real Numbers

The real numbers can be ordered and
represented in order on a number line

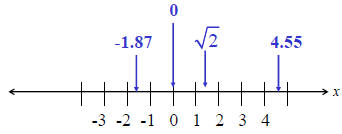
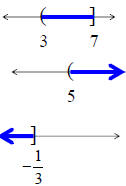
Inequalities, graphs, and notations

Inequality	Graph	Interval

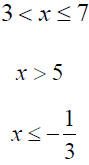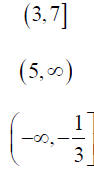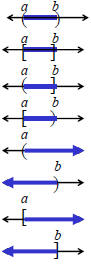
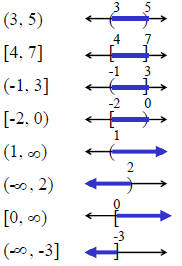
) or ( means not included in the solution
] or [ means included in the solution

Intervals

Interval	Graph	Example

Properties of Inequalities

If a, b, and c are any real numbers, then		Example
Property 1	If a<b and b<c , then . a <c	2 < 3 and 3 < 8, so 2 < 8.
Property 2	If a<b then . a +c< b+c	-5<-3,so -5+2<-3 +2 that is,-3<-1
Property 3	If a<b and c<0 then ac<bc	-5<-3,and 2>0,we have (-5)(2)<(-3)(2);that is ,-10< -6
Property 4	If a<b and c<0 then ab>bc	-5<4,and -2<0,we have (-5)(-2)>(4)(-2);that is,10>-8

Absolute Value


 

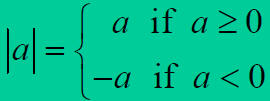
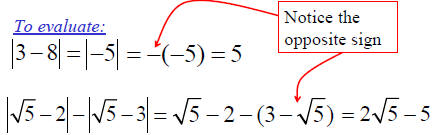
Absolute Value Properties

If a and b are any real numbers, then		Example
Property 5	l−a l= lal	l−4l = −(−4) = 4 = l4l
Property 6	la bl = lal lbl	l(2)(−3)l = l−6l = l2l l−3l
Property 7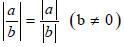
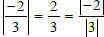Property 8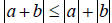

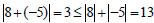Exponents

n,m positive integers	Definition	Example
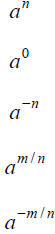	n factors

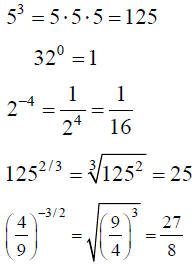Laws of Exponents

Law	Example

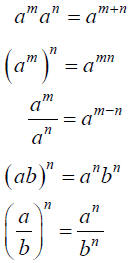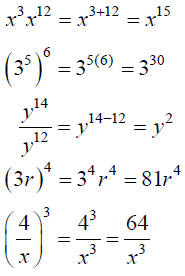Algebraic Expressions

• Polynomials
• Rational Expressions
• Other Algebraic Fractions

Polynomials

• Addition

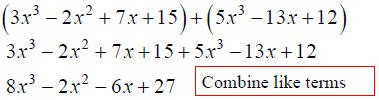
• Subtraction

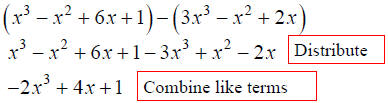
Polynomials

• Multiplication

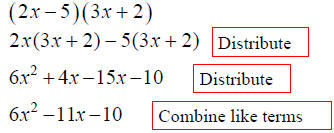
Factoring Polynomials

•Greatest Common Factor

• Grouping

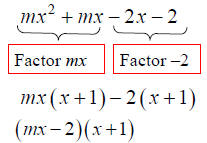
Factoring Polynomials

Difference of Two Squares:

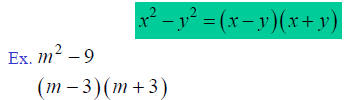
• Sum/Difference of Two Cubes:

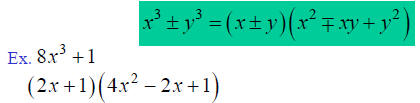
Factoring Polynomials

• Trinomials

Roots of Polynomials

• Finding roots by factoring

(find where the polynomial = 0)

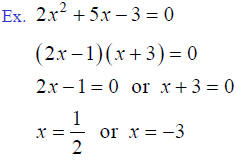
Roots of Polynomials

• Finding roots by the Quadratic Formula

• The Quadratic Formula:

If ax² + bx + c = 0 (a ≠ 0)

with a, b, and c real numbers,
then

Example

Using the Quadratic Formula:

Ex. Find the roots of 3x² + 7x +1= 0

Rational Expressions

Operation	P, Q, R, and S are polynomials
Addition
Subtraction
Multiplication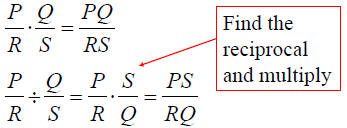
Division

Rational Expressions

Rational Expressions

• Adding/Subtracting

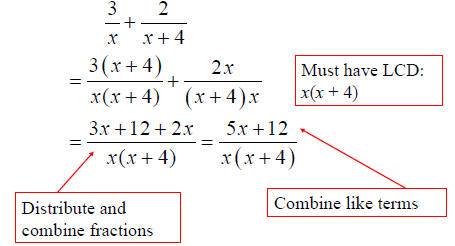
Other Algebraic Fractions

• Complex Fractions

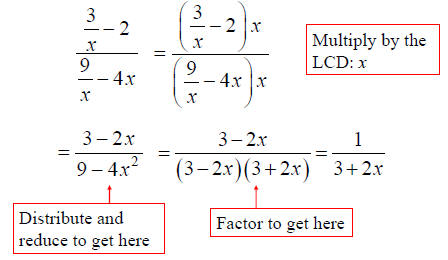
Other Algebraic Fractions

Notice:

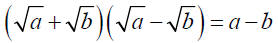
• Rationalizing a Denominator

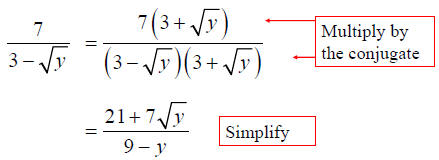
Cartesian Coordinate System

Cartesian Coordinate System

The Distance Formula

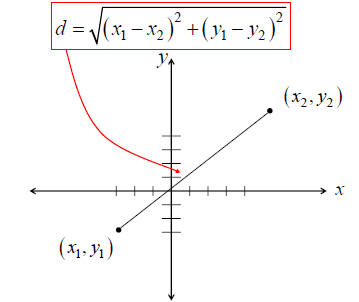
The Distance Formula

Ex. Find the distance between (7, 5) and (-3, -2)

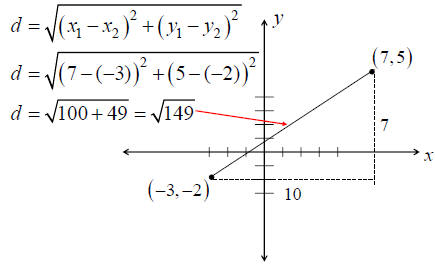
The Equation of a Circle

A circle with center (h, k) and radius of

length r can be expressed in the form:

(x − h)²+ ( y − k )²= r²

Ex. Find an equation of the circle with center at (4, 0) and radius of length 3

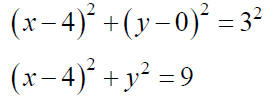
Straight Lines

• Slope
• Point-Slope Form
• Slope-Intercept Form

Slope – the slope of a non-vertical line
that passes through the points

(x₁,y₁)and (x₂,y₂)is given by:

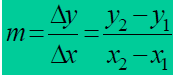
Ex. Find the slope of the line that passes through the points (4,0) and (6, -3)

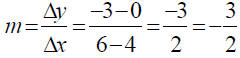
Slope

Two lines are parallel if and only if their
slopes are equal or both undefined

Two lines are perpendicular if and only if
the product of their slopes is –1. That is,
one slope is the negative reciprocal of the
other slope (ex. 3/4 a n d -3/4 ).

Point-Slope Form

An equation of a line that passes through
the point with slope m is given

by:
y − y₁ = m x − x₁

Ex. Find an equation of the line that passes through (3,1)
and has slope m = 4.

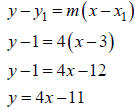
Slope-Intercept Form

An equation of a line with slope m and
y-intercept ( 0 , b ) is given by:

y = mx + b

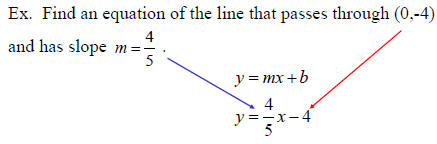
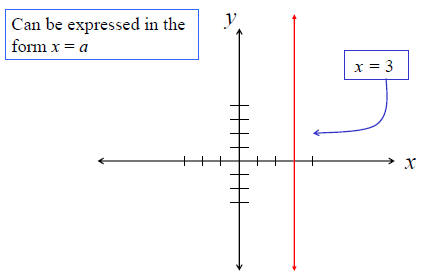
Vertical Lines

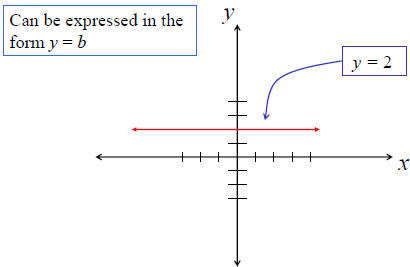
Horizontal Lines

Example
 

Find an equation of the line that passes
through (-2, 1) and is perpendicular to the line
y = 2x − 7.

Solution:

Step 1.Since the slope of the line y=2x - 7 is 2,

we have the slope of the perpendicular line is m=-1/2 .
 

Step 2.

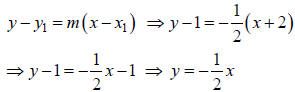
Example

Find an equation of the line that passes through
(0, 1) and is parallel to the line 6x + 2 y = 5.

Solution:

Step 1.We need to find the slope of the line

6x + 2 y = 5.

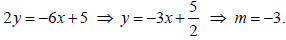
The slope of the parallel line is also m=-3.

Step 2.
Since m=-3 and b=1,