Home

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Measurements Significant figures Scientific Notation

Read the following scales

3 units
Reading

3.4 units
Reading

3.41 units
Reading

Uncertainty in
measurement

Read the following

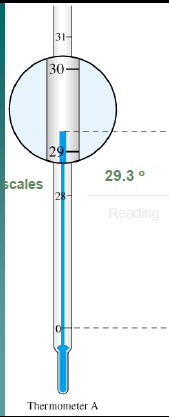
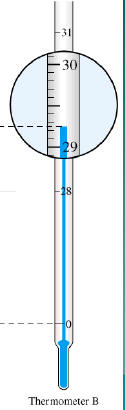
29.25°

Reading

Read the following scales

Uncertainity in a measured number

To determine the uncertainity in a number
–look at the last digit –this is the uncertain digit
–402.3 Last digit is 3 and is in the tenths place
The uncertainity is + 0.1
–402.34 Last digit is 4 and is in the hundredths place
The uncertainity is + 0.01

Uncertainity in a measured number

Examples: continued
–230 Last significant digit is 3. 3 is in the tens place
The uncertainity is + 10
This means our measurement is 230, 220 or 240

Errors in Measurement

Random errors are errors originating from
uncontrolled variables in the experiment.
Experimental values that fluctuate about the true value.
Systematic errors are errors originating from
controlled variables in the experiment.
-constant errors
-occur again and again
-affect the accuracy of the measurements can occur due miss-calibration of a measuring device
-are readings in variables such as temperature, pressure, flow, weight and alike

Driving down the thruway to MCC

Weight your car to the nearest 1 lb $50.00

Weight your car to the nearest 10 lb $15.00

Weight your car to the nearest 100 lb $2.00

Cont.

Weight Limit 2556 and we mean it!.

Car manual reads weight to be between 2421 to 2707
depending on # people in car and what’s in the trunk

At $2.00 station weight is 2600 which
means car weight is 2500-2700 lbs

At $15.00 station weight is 2550
which means car weight is 2540-2560 lbs

At $2.00 station weight is 2549
which means car weight is 2548-2550 lbs

Will the bridge collapse?

Discussion

Significant Figures

Significant Figures rules
•The digits 1 to 9 inclusive always count as
significant figures
14.23
3.112
244.62

Leading zeros and zeros that occur at the start of
a number , do not count for sig. figs. They only
indicate position
.004
.00036
0.00125

Zeros between nonzero digits count for sig.fig.
3.075
1005
.030078

Zeros at the end of the number are only
significant if they are after a decimal point
(trailing zeros)
100.030
50.0
.1000

If you can transform the number to scientific
notation and the zeros are lost, they were not
significant

93,000,000 = 9.3 x 10^7

How many significant figures are in
each of the following measurements?

24 mL	2 significant figures
3001 g	4 significant figures
0.0320 m³	3 significant figures
6.4 x 10⁴ molecules	2 significant fig
560 kg	2 significant figures

Significant Figures

Addition or Subtraction

The answer cannot have more digits to the right of the decimal
point than any of the original numbers.

	one significant figure after decimal point round off to 90.4
	two significant figures after decimal point round off to 0.79

Problems:

Add 5.62 + 0.0223 + 9.831
Least precise quantity is 5.62 1/100^thplace

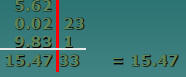
Add 0.02457 + 1.00001 + 0.003
Least precise quantity is 0.003 1/1000^thplace

Problems:
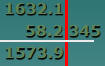
Substract 1632.1 -58.2345
Least precise quantity is 1632.1 1/10^thplace

Significant Figures

Multiplication or Division

The number of significant figures in the result is set by the original
number that has the smallest number of significant figures


3 sig figs	round to 3 sig figs


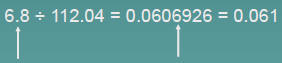2 sig figs	round to 2 sig figs

Significant Figures

Exact Numbers

Numbers from definitions or numbers of objects are considered
to have an infinite number of significant figures

The average of three measured lengths; 6.64, 6.68 and 6.70?

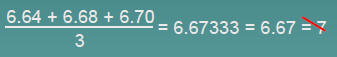
Because 3 is an exact number

Scientific Notation

The number of atoms in 12 g of carbon:

602,200,000,000,000,000,000,000

6.022 x 10²³

The mass of a single carbon atom in grams:
0.0000000000000000000000199

1.99 x 10^-23

N x 10ⁿ

Scientific Notation
consists of two parts.

Scientific notation: Adding exponents

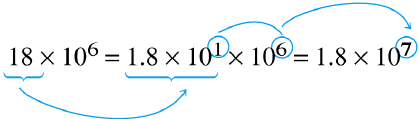
Express 18 as 1.8 x 10¹

Add exponents

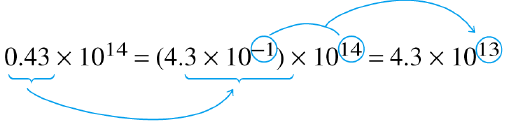
Express 0.43 as 4.3 x 10^-1

Add exponents

Scientific Notation

568.762	0.00000772
←move decimal left	→move decimal right
n > 0	n < 0
568.762 = 5.68762 x 10²	0.00000772 = 7.72 x 10^-6
Addition or Subtraction
1.Write each quantity with the same exponent n	4.31 x 10⁴+ 3.9 x 10³=
2.Combine N₁and N₂	4.31 x 10⁴+ 0.39 x 10⁴=
3.The exponent, n, remains the same	4.70 x 10⁴

Scientific Notation

1.86 x 10⁵would be the

Number.

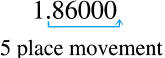
Scientific Notation
3.2 x 10²⁰

Scientific Notation
1.6 x 10^-3would be the number

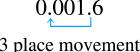
Scientific Notation
1.0 x 10^-7would be the number

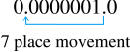
Scientific Notation

Multiplication

1.Multiply N₁and N₂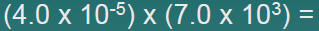
2.Add exponents n₁and n₂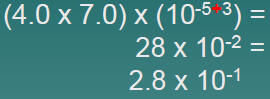
Division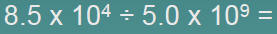
1.Divide N₁and N₂
2.Subtract exponents n₁and n₂

Accuracy–how close a measurement is to the true value

Precision–how close a set of measurements are to each other


accurate & precise	precise but not accurate	not accurate & not precise