Public Key Algorithms II

Overview

• Digital Signature Standard - DSS
• Zero-knowledge Proof Systems

Digital Signature Standard (DSS)

• By NIST, designed by NSA
  • Proposed in 1991, approved in 1994
  • DSA – algorithm
  • DSS – standard
• Related to El Gamal
• Speeded up for signer rather than verifier: smart cards
• Controversy RSA vs. DSS
  • When DSS was proposed a lot of investments were made in RSA
  • DSS a royalty free standard
  • DSS key size initially 512 later 1024
  • Designed by NSA

DSS Algorithm

• Generate public: p (512 bit prime) and q (160 bit
prime): p = k*q + 1
  • This is a very expensive operation, but not often
• Generate public g≠1: g^q = 1 mod p
  • Take a random h>1 get g = h
  • If g = 1, chose another h^(p-1)/q
• Choose long-term public/private key pair <T, S>,
with random S
  • T = g^S mod p for S < q

• Choose a per message public/private key pair
<T_m, S_m> with random S_m for message m
  • T_m = (g^S_m mod p) mod q
  • Calculate S_m^-1 mod q , so it won’t need to be done
in real time when signing a message
• Calculate a digest of the message d_m = SHS (m)
• SHS – a hashing function recommended by NIST for
use with DSS. SHS hashes to 160 bits

• Signature 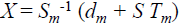mod q
• Transmit m, T_m, X
• Public key information T, p, q, and g are known
beforehand
• Verify:
  • Compute X^-1 mod q
  • Compute d_m
  • x= d_m X^-1 mod q
  • y= T_m X^-1 mod q
  • z = (g^x T^y mod p) mod q
  • if z = T_m, the signature is verified

Why Is DSS Secure

• No revealing of private key S
• Can’t forge a signature without S
• No duplicate messages with matched signature
• Can’t be tempered
• Need a per-message secret number (S_m)!
  • If S_m known, S can be computed
  • Two messages sharing the same S_m can reveal
S_m, and thus S

Per message Secret Number

• How is the private key exposed if the secret number
per message is known?
• If S_m is known, one can compute:
  • (X_m S_m – d_m) T_m^-1) mod q = S mod q
• How is the private key exposed when two messages
share the same secret number?
  • If m and m’ are signed using the same S_m
  • One can compute:
(X_m – X_m’ )^-1  ( d_m - d_m’ ) mod q = S_m mod q
• How to generate random numbers?

How Secure are RSA and
Diffie-Hellman ?

• The security of RSA is based on the difficulty of
factoring
• The security of Diffie-Hellman is based on the
difficulty of resolving discrete log problems
• It has been proved that they are equivalently difficult
• The best known algorithms to resolve them are
subexponencial but superpolynomial
• That’s why a larger key size is required (1024bits)
compared to secret key (80 bits)

Elliptic Curve Cryptography ECC

• No known subexponential algorithms to break ECC
• So it is secure with much smaller key – improve
performance
• An elliptic curve is a set of points satisfying an
equation of the form:
y^2 + ax + by = x^3 + dx +e
• Mathematical operation on two points in the set will
always produce a point in the set

Zero-Knowledge Proofs

• Alice: “I know the ingredients in McDonald’s secret
sauce”
• Bob: “No, you don’t”
• Alice: “Yes, I do”
• Bob: “Prove it”
• Alice: “All right. I’ll tell you.” She whispers in Bob’s
ear”
• Bob: “Now I know it too. I will post in my web page”
• Alice: “Oops”

The Zero-knowledge Cave

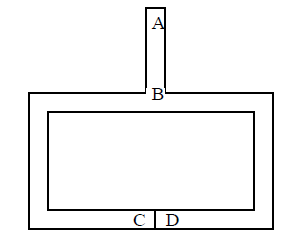
The Zero-knowledge Cave

• 1. Bob stands at point A
• 2. Alice walks all the way into the cave, either to point
C or D
• 3. Bob walks to point B
• 4. Bob asks Alice to
  • Come out of the left passage
  • Come out of the right passage
• 5. Alice complies by using the magic word to open the
door C or D
• 6. Bob and Alice repeat steps 1-5 n times.

Zero-knowledge Proof Systems

• Prove knowledge without revealing it
• RSA signatures
• Graph isomorphism: rename vertices
  • Alice: graph A and B ~ A
  • Public key: graphs A, B
  • Private key: mapping between vertices
  • Alice: create G_i and sends to Bob
  • Bob → Alice: how did A or B → G_i ?
  • Zero-knowledge: Bob knows nothing about the mapping
between A and B
  • Fred can generate G_i from either A or B, but not both

Zero-knowledge Proofs:
Fiat-Shamir

• Alice: public key <n, v>, n=pq, private key s
  • Alice selects random number s, and computes v=s^2
mod n
• Alice chooses k random numbers r₁ …, r_k
• Alice sends r_i^2 mod n
• Bob chooses a random subset 1 of r_i^2, the rest is
subset 2
  • For subset 1, Alice sends sr_i mod n, and Bob
verifies (sr_i)^2 mod n = vr_i^2 mod n
  • For subset 2, Alice simply sends r_i mod n
• Finding square root mod n is hard

• Suppose Fred wants to impersonate Alice
• Fred can compute squares mod n but cannot take
square roots mod n
• Fred can send random r and compute r^2, so he can give
correct answers for subset 2, but not for subset 1
• So what the purpose of subset 2? Why isn’t the
protocol simply that Alice sends pairs (r_i^2, sr_i)?

• If only (r_i^2, sr_i) was used
  • If Fred has overheard Alice providing (r_i^2, sr_i), he
can impersonate Alice.
• But because both subsets are needed
  • Even if he knows subset 1 + answer and subset 2 +
answer, the probability of having the new subset 1’
equal to subset 1 is very small
  • For each I the probability is 50%, for the whole
subset (30) no chance to impersonate, on in ten
billion

Summary

• Digital Signature Standard - DSS
• Zero-knowledge Proof Systems