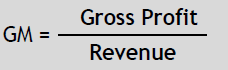Week 4 Math

Agenda

•Why Do They Try to Trick Us with Math?
•Fundamental Math Concepts
•Intermediate Math Concepts
•Advanced Math Concepts
•Group Casing Exercises

Why numbers matter in the case interview

“I know that numbers mean everything in business. But why are math skills important in interviews if I’ll have a calculator at work?”

–Basic skills demonstrate that you can think methodically and understand mathematical relationships
–Firms want to see if you can apply numerical data to clarify a business story and substantiate a set of recommendations
–Interviews force you to articulate the logic of your calculations
–Tedious math problems test your poise under pressure

So You Don’t Like Math.

How often do the more complex math concepts really show up in cases?

Answer: Complex math shows up less often than basic division, percents, etc. BUT, you never know whey you will get a case with tricky math

How should you prepare?

•Practice basic math –multiplication, division, decimals, percentages
•Get familiar with the basic equations for a short list of more complex concepts
•Develop an understanding of the purpose of more complex math concepts, and know the general impact of answers of different magnitude

Agenda

•Why Do They Try to Trick Us with Math?
•Fundamental Math Concepts
•Intermediate Math Concepts
•Advanced Math Concepts
•Group Casing Exercises

Fundamental Math Techniques

•You MUST know these and practice them:
–Long division
–Multiplication
–Addition
–Subtraction
–Basic fractions and simplification
–Percentages
–Algebra, solving for X

Large Numbers

•Difficulty:
–Easy to make mistakes (especially number of zeroes)
–Time-consuming to write (e.g. $25,000,000)
•Solution:
–Symbol of magnitude: $25M
–Scientific notation: $2.5 x 10⁷
–1K = 1.0 x 10³… 1M = 1.0 x 10⁶… 1B = 1.0 x 10⁹
–Working with scientific notation:
  •Multiplying: Multiply coefficients and add exponents.
  •Adding: Exponents must be equal!

Percentages

•Difficulty:
–Takes different forms, each using similar language

•Solution:
–Part/whole concept (% = part/whole)
–Understand “percent of” and “percent increase”
–Understand markup and margin

•Tips:
–Practice!
–Purplemath.com covers all the bases

Percentages: you thought they were easy?

•Question:
–Your company sells ice cream in a market where customers are segmented by favorite flavor. 70% of your customers belong to the vanilla segment. Your customers make up 3.6% of the market. 10% of the customers in the market prefer vanilla ice cream. What percentage of the vanilla customers in the market does your company serve?

•Answer:
–0.7 * 0.036 / 0.1 = 0.252We are introduced to three overlapping groups of people: “your customers,” “vanilla customers,” and “the market.” We are asked how a particular overlap –the intersection of all three groups –compares to one of the groups –the vanilla customers. Note: everything is in percent terms relative to the market.
–Step 1: find the “part”: 70% of 3.6% = 2.52%. Step 2: find the “whole”: we already know it‟s 10%. Step 3: divide part/whole: 2.52% / 10% = 25.2%

Agenda

•Why Do They Try to Trick Us with Math?
•Fundamental Math Concepts
•Intermediate Math Concepts
•Advanced Math Concepts
•Group Casing Exercises

Market Sizing -Segmentation

•Difficulty:
–How do you size a market quickly and sensibly?

•Solution:
–Start with a known population
–Divide the population into segments according to [age,income,etc]
–Pick percentages of each segment who belongs in your market

•Tips:
–Use 300M for US Population
–Use manageable round numbers for bracket sizes and percentages
•300/4 = 75 … 75/3 = 25

Market Sizing –Segmentation Example

•Question:
–How many cups of coffee are sold in the US every year?

•Answer:
–Total cups/day * days/year
–The US Pop is 300M. Let‟s bracket by age in groups of 20-year spans and assume an even distribution
(75M in each bracket).

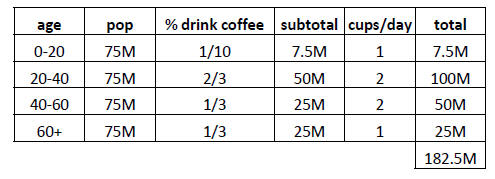
182.5M * 365 =66.6B cups/yr

13Market Sizing

Rule of 72

Rule of 72 helps to answer the following questions

•How long it takes to double your savings (approximately) for a given saving rate
Start with the number 72.
Divide by the rate of return you expect to earn
You will get your investment horizon, or number of years you need to double your investments

•What rate of return should you get if you want to double your money in a given number of years
Start with 72.
Divide by the number of years your want to have your return doubled
You will get the AFTER-TAX COMPOUND ANNUAL RATE OF RETURN you would have to earn

Question

•In investor knows she can earn 16% of return on her money. How long it will take to double the investment?

 

•In investor needs to double his money in 3 years (legally). What is the rate of return must he earn to do this successfully?

 

Solution

•In investor knows she can earn 16% of return on her money. How long it will take to double the investment?

72/16 = 4.5 years

•In investor needs to double his money in 3 years (legally). What is the rate of return must he earn to do this successfully?

72/3 = 24%

Estimation

•What's 14% of 2.3 million?

 

Solution

•Estimation
–Look for 15% of 2.3MM
–10% of 2.3MM = 230K
–50% of 230K = 115K
–Answer ~ 345K
–(You could then easily reduce your estimate to 325K by subtracting 20K.)

•Calculation
–Scale down and scale up
–10% of 2.3MM = 230K
–1% of 2.3MM = 23K
–4% of 2.3MM = 92K
–230K + 92K = 322K

Zeros and Decimals

•What‟s .0003% of 2.6 billion?

 

Solution

•Estimate/Calculation
–Where does the decimal go?
–Find .0001% and scale up.
–Dividing .0001 by 100 gives a % multiplier of:

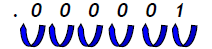
–From R to L, the decimal point has moved 6 places.
–Moving the decimal point left 6 places in 2.6 billion = 2,600
–2,600 x 3 = 7,800

Percentage

•What‟s 14% of 2.3 million?

 

Percentage Solution

•What‟s 14% of 2.3 million?

•Estimate
–Look for 15% of 2.3MM
–10% of 2.3MM = 230K
–50% of 230K = 115K
–Answer ~ 345K
–(You could then easily reduce your estimate to 325K by subtracting 20K.)

•Calculation
–Scale down and scale up
–10% of 2.3MM = 230K
–1% of 2.3MM = 23K
–4% of 2.3MM = 92K
–230K + 92K = 322K

Problem

In 2030 the world will have 1.2 billion cars. This is one vehicle for every 6.7 people projected to be on the planet at 2030. This is also 92% more cars then we have on the road today.

•How many vehicles are on the road today?

•If the ration of cars to people will be half of the one we have today, how many people are in the world today?

Solution

24Solution
Solve: 625 million cars
X*1.92 = 1,200,000,000
Estimate: 1,200,000,000/2 = 600 million , You are dividing by a little less then 2, so it will be a little more then 600. Estimate solution is 630,000,000.

Solve: 6.979 Billion
X*1.92=6.7*2
X=13.4/1.92 = 6.9
Estimate: From (X*1.92=6.7*2) you should see that the number a little higher then 6.7. Estimate solution is 7 billion.

(Btw, current world population is 6.7 billion)

Gross Margin

CONCEPT	•Gross margintells us how much of every dollar earned by the firm, after paying direct fixed and variable costs, is available to cover overhead costs and serve as a buffer to unknown items
	•More simply, GM tells us how many of our sales dollars are profit CONCEPT

Gross Margin Equation	Components of the GM Equation
	Gross Profit = Revenues –(FC + VC)

GM

•Revenue = 3.5MM. Cost = 2.1MM. Find GM.

Solution

GM = (R –C) / R

•Estimate
–1.5 / 3.5 is a little under 50%.
–Answer ~ 45%

•Calculation
–(3.5 –2.1) / 3.5
–1.4 / 3.5
–Answer = 40%

Agenda

•Why Do They Try to Trick Us with Math?
•Fundamental Math Concepts
•Intermediate Math Concepts
•Advanced Math Concepts
•Group Casing Exercises

Net Present Value

CONCEPT	•Net present value tells us whethera particular investment will add value to our company. If NPV is positive, make the investment
	•Literally, NPV is a comparison of the expected future cash inflows from an investment to the expected cash outlay(s) needed to finance the project

Step 1: PVof Cash Inflows	Step 2: FindNPV
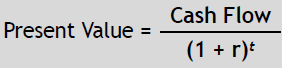	* Initial Investment represents the PV of all cash outflows needed to finance the project

Example of Present Value Discounting

Common discount rates and periods that show up in cases

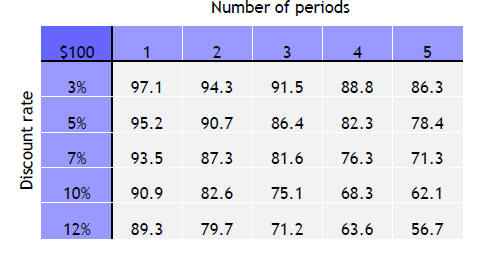
Remember:

•The larger the discount rate, the smaller the present value
•The greater the number of periods, the smaller the present value
•Thelarger the discount rate, the greater the risk premium applied to the potential investment
•Usethe Rule of 72when possible
•Round and estimate when possible

Present Value of an Annuity

CONCEPT	•The present value of an annuity, also known as the perpetual growth formula, tells us the value today of a series of cash flows that expect to last forever into the future
	•The perpetual growth formula can help us value a company

Basic Equation	Definition of Terms
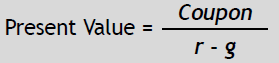	Coupon = the regular cash flow payment r= discount rate g= growth rate

Customer Lifetime Value

CONCEPT	•Customer Lifetime Value is the present value of all future streams of profits that a customer generates over the life of his/her business with the firm
	•CLV tells us how much we can spend to “acquire” a new customer

Basic Equation	Definition of Terms
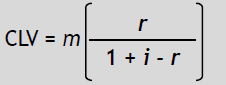	m= margin from each customer r= retention rate i= discount rate

ACCOUNTING RATIOS

Why it is important to know the key ratios:

•Used to evaluate the overall financial condition of a corporation
•Financial ratios allow for comparisons
 •between companies (when firms use the same accounting methods)
 •between industries
 •between different time periods for one company
 •between a single company and its industry average

What do you want to remember

•SOLVENCY
•LIQUIDITY
•PROFITABILITY
•OPERATING EFFICIENCY
•FINANCIAL LEVERAGE

Values used in calculating financial ratios are taken mostly from the

BALANCE SHEET, INCOME STATEMENT, CASH FLOW STATEMENT!

When to use in a case

•When you are given financial statements to analyze
•When you are trying to decide whether a company should invest in a new project now (a liquidity issue) or will it stay in business or be able to take on some extra debt (solvency issue)

Solvency Measurements

WHY?

To be able to assess the ability of a corporation to meet its long-term fixed expenses and to accomplish long-term expansion and growth.

•A ratio used to measure a company's ability to meet long-term obligations. The solvency ratio measures the size of a company's after-tax income, excluding non-cash depreciation expenses, as compared to the firm's total debt obligations. It provides a measurement of how likely a company will be to continue meeting its debt obligations.

Liquidity Measurements

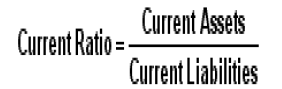
•Current Ratio answers the question whether the firm can meet its short term obligations.

•Quick Ratio answers the question whether a firm can meet short term obligations tomorrow.

Problem

•At December 31 a company's records show the following information:
 •Cash $ 10,000
 •Accounts Receivable 30,000
 •Inventory 80,000
 •Prepaid Insurance 6,000
 •Long-term Assets 200,000
 •Accounts Payable 30,000
 •Note Payable due in 10 months 25,000
 •Wages Payable 5,000
 •Long-term Liabilities 70,000
 •Stockholders' (Owner's) Equity 196,000

What are the Current Ratio and the Quick Ratio?

Solution

•Current Assets -$126,000:
 •Cash $ 10,000
 •Accounts Receivable 30,000
 •Inventory 80,000
 •Prepaid Insurance 6,000

•Current Liabilities
 •Accounts Payable 30,000
 •Note Payable due in 10 months 25,000
 •Wages Payable 5,000

•126,000/60,000 = 2.1

Liquidity measurements cont.

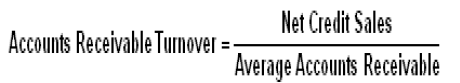
•The larger the ratio, the shorter the collection period is for receivables, meaning that the company gets cash more quickly

Account receivable collection period = 365 days/accounts receivable turnover ratio

•Reflects the number of days on average it takes the company to collect accounts receivables

Profitability Measurements

Why?

Give an idea of how likely it is that a company will turn a profit, as well as how that profit relates to other important information about the company.

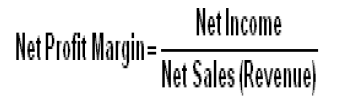
•Decreasing profit margins year over year -changing market conditions, increasing competition , rising costs. Also, if a company's profit margin is out of line compared to the rest of its industry, it is worth the extra effort to find out why.

Profitability Measurements cont.

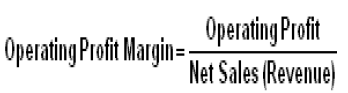
•Operating margin is a measurement of what proportion of a company's revenue is left over after paying for variable costs of production such as wages, raw materials, etc.

•look at the change in operating margin over time and to compare the company's yearly or quarterly figures to those of its competitors. If a company's margin is increasing, it is earning more per dollar of sales. The higher the margin, the better.

For example, if a company has an operating margin of 12%, this means that it makes $0.12 (before interest and taxes) for every dollar of sales.

Operating Efficiency Measurements

WHY?

Asset Turnover Ratio = Net Sales/Average Total Assets

•The higher is the ratio, the more efficiently a firm is using its assets

Rate of Return on Investments (known as ROI) = Net Income/Total Average Assets

ROI = Profit Margin*Asset Turnover Ratio

Financial Leverage

WHY?

To increase return on Equity

Financial Leverage = Average Total Assets/Average Common Stockholder‟s Equity

•Amount of assets financed by stockholders

Rate of Return

Rate of return on common stockholder „s equity
=
Net Income/Average Common Stockholder‟s Equity
=
Profit margin*Asset turnover*Leverage

Agenda

•Why Do They Try to Trick Us with Math?
•Fundamental Math Concepts
•Intermediate Math Concepts
•Advanced Math Concepts
•Group Casing Exercises