Introduction to Symbolic Computation

2.4 Calculations in MATLAB

Operators you can use are the following:

+ addition

- subtraction

* multiplication

/ right division (a / b means a * inv(b) )

\ left division (a \ b means inv(a) * b )

You can apply these operators on numbers as well as on matrices.

If you want to compute something in MATLAB, then you type the expression after the prompt.
e.g.:

>> x + 2 enter

MATLAB answers :

ans =

2,6500

The result is by default assigned to the variable ans ( = answer).

You can also assign the result to a variable.
e.g.:

>> y = x + 2 enter

Then MATLAB answers :

y =

2,6500

2.5 Some elementary functions in MATLAB
log, exp, sin, cos, tan,. . .

The argument has to be enclosed in round brackets.
e.g.:

>> log(1) enter

returns

ans =

0

abs returns the absolute value

round returns the nearest integer number

2.6 Matrix operations

inv(a) computes the inverse of a
det(a) computes the determinant of a
cond(a) computes the condition number of a
rank(a) computes the rank of a
size(a) returns number of rows and columns of a
norm(a) computes the norm of a vector or a matrix
eye(n) gives the n-dimensional unit matrix
diag(d) returns a diagonal matrix with elements d(i) on its diagonal
rand(n;m) generates a random n-by-m matrix
orth(a) returns an orthonormal basis for the range of a
lu(a) returns the factors of the LU-decomposition of a
After typing

>> [l, u] = lu(a) enter

MATLAB returns two matrices l and u: l is a (eventually permuted) lower triangular matrix with ones
on the diagonal and u is an upper triangular matrix.

To solve a linear system ax = b, you can use the MATLAB division

>> x = a \ b enter

eig(a) computes eigenvalues and eigenvectors.

After typing eig(a) MATLAB gives you a vector with all eigenvalues of a.
To obtain the eigenvectors as well, you type

>> [v; d] = eig(a) enter

The two matrices v and d on return have the following meaning: d is a diagonal matrix with the
eigenvalues of a on its diagonal, and v contains in its columns the eigenvectors of a. Without roundo®,
a * v == v * d.

An interesting MATLAB function is the command flops. flops returns the number of floating point
operations, performed in a session. With flops(0) you initialize this counter to zero. This is useful to
measure the amount of computational work needed for one or a sequence of operations.

2.7 Programs

You can collect a sequence of MATLAB commands in one file, which should have the `.m' extension. This
sequence of commands is then executed when you type in the name of that file (without the extension).
To ensure that MATLAB will find your program, you may have to adjust MATLAB search path with the
command path Typing path displays MATLAB's current search path. To append a directory to this path,
type path(path,'c:\temp\my files') for instance.

3 Assignments

1. Type tour in a MATLAB session, follow the Intro to MATLAB link and browse through the various
aspects that interest you.

2. Type in u = [2 3 1 4]; v = [4 3 2 1]; w = [1 2 3 4];
Give MATLAB commands to create a matrix a that has as rows u, v, and w.
The matrix a defines the augmented matrix of a 3x3 linear system with right hand size vector in its
fourth column. Compute its reduced row echelon form with rref.
What is the solution of the corresponding linear system? Verify!

3. The linear system Ax = b is defined by

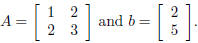
Give the MATLAB commands to enter A and b, to find x, the solution to Ax = b, and finally to
compute the norm of b - Ax.

4. Type a = [1 2 3; 4 5 6; 7 8 9], followed by [l, u] = lu(a). Test whether l * u equals a. Notice that u is
upper triangular. Explain why l is not lower triangular. (hint: type help lu.)

5. Generate a random 6 × 6 matrix a and compute the LU-decomposition of a, storing the factors of the
LU-decomposition in the matrices l and u.

(a) Test whether l * u equals a by computing r = a - l * u. Is r the zero matrix? Interpret the results
and explain what went wrong.
(b) The determinant of a product of two square matrices is the product of the determinants of the
factors in the product. Test whether det(a) = det(l) * det(u). What is the most efficient way to
compute the determinant of a matrix, given its LU-decomposition?

6. Generate a random 6×6 matrix a and a random column vector b. To solve the system ax = b, we will
compare the difference in floating point operations between various methods.

method 1, taking the inverse : Type flops(0); x = inv(a) * b; flops.
method 2, reduced row echelon form : Type flops(0); rref([a b]); flops.
method 3, the backslash operator : Type flops(0); x = a\b; flops.

Compare the results of the three flops operations. What can you conclude?

7. For increasing values of the dimension n = 2, 3,…,10, compare n³ with the flops needed to perform
an LU-decomposition in the following way. For n = 2, 3,…, 10, generate a random n × n matrix a
execute flops(0); lu(a), and flops. For each value of n, write the output of flops in a table, next to
the values for n³. In the last column, write the quotient of flops divided by n³.

Write the results in a table formatted like the one below:

n	n3	flops	flops=n3
2 3 ... 10

What can you conclude about the amount of computational work needed for LU-decomposition?

8. Type in the following:

>> a = rand(6, 6); b = rand(6, 1); enter
>> for i = 1 : 20 enter
b = a * b;   enter
b = b/norm(b); enter
end; enter

Compare the vector b with the eigenvectors of a. What do you observe?