FRACTION OF A WHOLE NUMBER

1. Mathematics
Fraction of a Whole Number (students will demonstrate knowledge using the following methods)
▪ Create a model of a fraction of a number using connecting cubes, red/white counters, and 1cms
square grid paper.

▪ Solve fractions of a number using the mathematical algorithm of whole number is
(whole number * numerator) ÷ denominator or

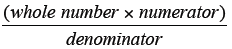
2. Grade Level: 6^th Grade

3. Manipulatives or Tools Needed: connecting cubes, red/white counters, 1cm square grid paper
(blackline master #35), colored pencils, scissors

4. Before Stage (estimated time -- 10 minutes)
▪ Pre-requisite Skills: multiplying whole numbers, comparing and understanding fractional parts,
adding/subtracting fractions, simplifying fractions, changing improper fractions to mixed numbers and vise
versa, multiplication terminology (of means to multiply).
▪ Related Tasks: Students work in groups of 4 according to the table arrangement. Tasks are shown by
teacher reading them out loud and writing number sentences on the board.

Task 1: Demonstrate 3*5 using each a) connecting cubes, b) red/white counters, & c) 1cm square grid paper.
(Walk around to check each group’s models; go over what was done & possible interesting methods students might use)
What does the model represent? (3 groups/rows of 5) The first factor tells how much/how many groups/rows of
the second factor you have. Now demonstrate 5*3 using methods a, b, & c. What does this represent? (5
groups/rows of 3)

Task 2: Demonstrate 1/3 using each a) connecting cubes, b) red/white counters, & c) 1cm square grid paper.
(Walk around to check each group’s models) Now demonstrate 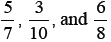using any of the three methods.
(Have students share their models)

5. During Stage (estimated time -- 25 minutes)
Task 3: Ask students to work with their partner & another set of partners (four students total per group), using
the manipulative and tools they have been given, to create a model of 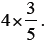. Remind students to think about the
problems the class did previously to help them figure out how to solve the problem. Tell students that they will
be expected to share their results with the class, so they need to fully understand the model they create. When
students have figured out their model, tell them to choose a spokesperson for their group.

Discussion: One group at a time, the groups’ chosen spokesperson stands and explains their group’s
model/method to the class. The class can gather around the group’s work area if necessary. See how many
different methods students found for multiplying a whole number by a fraction.
Prediction: I anticipate students struggling with this task, because of their lack of exposure to and use of
manipulative and models. If they struggle, I will direct them to first represent the whole number. Then ask
them how many parts each whole needs to be divided into. (hint: look at the denominator; 5 parts) Once students
receive that hint, they should be able to proceed to figure out the model. If this does not work, help the students
to draw out a model of four rectangles, divided into 5 parts, with 3 parts of each rectangle shaded.

6. After Stage (estimated time -- 15 minutes)
Summarize & Explain: Ask students if they have noticed a pattern of how to solve this and other similar
problems mathematically. If a student seems to have a valid method, ask them to explain it on the whiteboard
for the rest of the students. After all students have shared their ideas, explain to them the algorithm using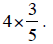

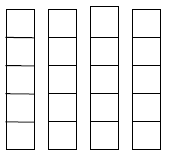
The whole number 4 tells you how many wholes rectangles you may have. Draw 4
rectangles.

The denominator of the fraction tells you how many parts each rectangle has.
Divide each rectangle into 5 sections to represent fifths.

The numerator tells you how many sections of each rectangle to shade. Shade 3
fifths of all 4 rectangles.

Multiply to find the number of shaded parts (3 parts x the 4 wholes). Represent the
shaded parts as a
fraction.

Simplify if possible.

Assign Practice: Ask students to work problems (p. 271) 1, 2, 11, & 23 on their own. After they have finished
them, they will get back into their groups and compare answers. The students will do their best to correct others
misunderstandings. If they have questions, I will help them. If it sounds like the students need more
instruction, do so. Otherwise assign the following problems to work on during class: 3-8 (using a model to find
answer), 12-15, 16-27.

7. What Comes Next?
▪ Students will build on their knowledge of multiplying a whole number by a fraction in following lessons
by learning to multiply fractions, and later on, divide fractions.
▪ Students will be given practice worksheets throughout the week and be instructed to solve the problems
using both the algorithm and some sort of drawn model.