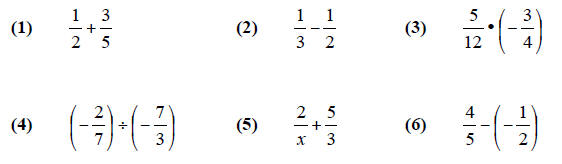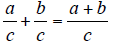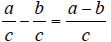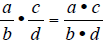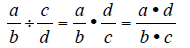- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Fractions
The thing that strikes me most about students and
fractions is the misuse of “shortcuts”
and the procedures required for each operation. I always begin with simplifying
fractions. Because of the future algebra class, particularly rational
expressions, heading
their way, I teach simplifying by factoring. It’s really difficult to simplify
polynomial
numerators and denominators without factoring.
Students really need to understand prime factorization to
accomplish simplification of
fractions. I hear students say that the twos will cancel out. This is actually
not true.
They really divide out for one.
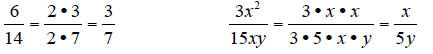
The one topic of fractions that seems to try many students
is that of common
denominator. Students should be reminded of the procedures for each operation.
The
only operations requiring a common denominator are adding and subtracting.
Multiplication and division do not require common denominators.
| Rule: To Add Two Fractions
|
Rule: To Subtract Two Fractions
|
| Rule: To Multiply Two Fractions
|
Rule: To Divide Two Fractions
|
Before practicing with negative fractions, it might be
wise to check the basic fraction
understanding from the previous rules.
Combine and simplify the fractions.
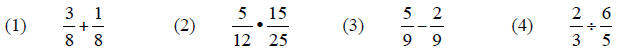
answers:
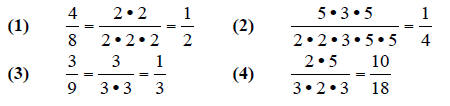
After checking for the most basic use of the rules, the
idea of common denominator and
equivalent fractions must be addressed.
For equivalent fractions, I like to use a number line in
the following way. I have the
students draw three number lines. I then have them label from zero to one. On
the first
number line, I have them put one mark exactly between zero and one. On the
second
line, I have them put the one mark in the middle and then one mark in the middle
of the
two resulting segments. One the third line, they do the same, except they then
bisect each
of the four segments. Then I ask them how many segments they have traveled to
the
middle. We put this over the total number of segments. It becomes visually clear
to
them. This exercise suggests that a fraction can look different from another,
yet still have
the same numerical value on the number line.
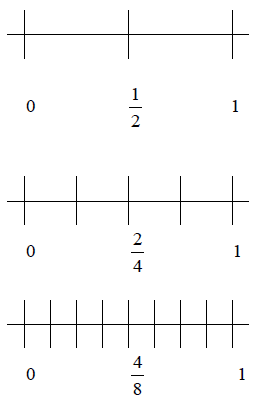
When first working with equivalent fractions, I like to
start with a particular fraction and
then ask them to write the equivalent fraction with a given denominator.
For instance, find the equivalent fraction to 2/5 that has a denominator of 20.
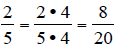
To build fractions to “higher terms,” use multiplication
in the numerator and the
denominator.
Find the equivalent fraction to 20/30 that has a denominator of 15.
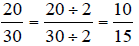
To reduce fractions to “lower terms,” use division in the numerator and the denominator.
The previous is different from reducing to “lowest terms.”
Lowest terms would leave no
common factors at all between the numerator and denominator.
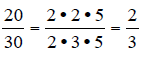
After introducing the idea of equivalent fractions,
students are ready to find the LCD
(least common denominator). There are so many ways to do this, but I find that
factoring
works best when dealing with variable factors.
To add 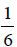 and
and
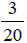 we need a common denominator.
we need a common denominator.
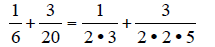
By rewriting with factored denominators, we can see
missing that need to be multiplied
into the denominator and numerator of each fraction.
From above, we can see that the first denominator needs
one factor of 2 and one factor of
5 to match with the second denominator. The second denominator needs one factor
of 3
to match up with the first denominator.
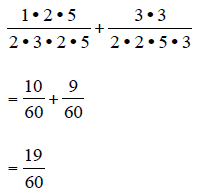
This works especially well with fractions containing variables.
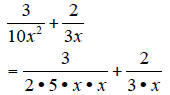
The first denominator needs one factor of 3. The second
denominator needs one factor of
2, one factor of 5, and one factor of x.
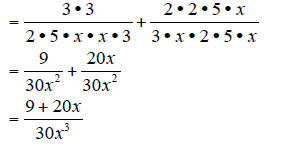
Practice Problems: