Functions

Equal Functions

Two functions f and g are equal if they have the same domain D, and f(d) = g(d) for all d in D.

Inverse Functions

Let f be a one-to-one correspondence from the set A to the set B. The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f(a) = b. The inverse function of f is denoted f -1. Thus, f -1(b) = a when f(a) = b, so f -1(f(a)) = a.

As we observed, the function f(x) = x + 1 from the set of integers to the set of integers is a
bijection. To reverse the correspondence, let y = f(x) = x + 1. Thus, we know that x = y – 1.
Consequently, f ^-1(y) = y – 1.

Note that not all functions have an inverse. A one-to-one correspondence is called invertible since
we can define an inverse of this function. However, a function is not invertible if it is not a one-to-
one correspondence, since the inverse of such a function does not exist. For example, the
function f(x) = x² from the set of integers to the set of integers is not invertible since it is not one-to-
one. Since f(-1) = f(1) = 1, the inverse of f would have to assign two elements to 1, which
violates the definition of a function. Hence, an inverse of f cannot exist in this case.

Composition of Functions

Consider two functions: successor as applied to integers, and a sqr (“square”) function. If we take
the output of the successor function and use it as input to the sqr function, the two functions are
operating together. They take as input an integer n, add one to it and then square n+1. We call this
a composition of two functions.

Let g be a function from the set A to the set B and let f be a function from the set D to the set C (where B is a subset of D). The composition of f and g, denoted by (f o g), is a function defined by: (f o g)(a) = f(g(a)) where a is an element of A. f o g may also be read "f circle g".

Here is a diagram to illustrate (in this case B = D):

So (f o g)(1) = y, (f o g)(2) = y, and (f o g)(3) = z.

always true that g(f(a)) = f(g(a)). Indeed, for a simple example of this, consider the case where g
has the set A as a domain and g has the set D as a domain, and the sets A and D contain no
elements in common. Then, while f(g(a)) may be defined, g(f(a)) is undefined, since f does not
operate on element a. In the diagram above, we cannot form g o f, because the co-domain of f is
not a subset of the domain of g. f always produces a result in the set {x, y, z}, and g does not
operate on these values.

Notice also that in the successor-sqr example, the composition is not commutative since (n + 1)² ≠
n² + 1 (except for n = 0).

As an additional example, let f and g be functions from the real numbers to the real numbers
defined as follows:

f(x) = 2x + 3
g(x) = 3x + 2

The composition of f and g is: (f o g)(x) = f(g(x)) = f(3x + 2) = 2(3x + 2) + 3 = 6x + 7
The composition of g and f is: (g o f)(x) = g(f(x)) = g(2x + 3) = 3(2x + 3) + 2 = 6x + 11

Thus both compositions are defined, but (f o g)(x) ≠ (g o f)(x).

A Few Important Functions

Now that we have all the definitions out of the way, there are a few functions that appear on
occasion in computer science that are worth specifically identifying.

Identity Function

Let I be a function from the set A to set A defined by I(a) = a for all a in A. The function I is called the identity function.

Floor Function

The floor function assigns to the real number x the largest integer that is less than or equal to x. The floor function applied to x is denoted .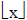

Ceiling Function

The ceiling function assigns to the real number x the smallest integer that is greater than or equal to x. The floor function applied to x is denoted .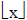

Examples:

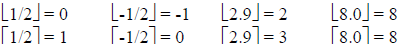
Proofs with Functions

Here are some examples of proofs with functions.

Problem: Prove: if f is a function from set A to set B that is a one-to-one-correspondence, then the
inverse function f ^-1 is one-to-one and onto (i.e., it is also a one-to-one correspondence).

Proof: First we show f ^-1 is onto. If a is in A, then since f is a function, there is a b in B such that
f(a) = b. Hence, by definition of inverse function, f ^-1 (b) = a, where b is in the domain of f ^-1 and a
is in the co-domain of f ^-1. Note that for any element a in A, f ^-1 (b) = a must hold for some b in B
in order for f ^-1 to be the inverse function of f. As a result, f ^-1 is onto (the set A).

Now, we show f ^-1 is one-to-one. Assume that some b' and b exist in B such that f ^-1 (b) = f ^-1 (b') =
a. If this is true, then f(a) = b and f(a) = b'. But since f is a function, it implies that b = b'
(otherwise, f would violate the definition of a function). Since b = b' in all such cases, it follows
that f ^-1 (b) = f ^-1 (b') implies that b = b'. Thus, f ^-1 is one-to-one (by the definition of one-to-one).
QED.

Problem: Let g be an invertible function from A to B and f be an invertible function from B to C.
Prove or disprove: (f o g) ^-1 = g ^-1 o f ^-1.

Proof: First, note that g and f are bijections, that (f o g) is a bijection from A to C, and thus
(f o g) ^-1 exists and is a bijection from C to A. (Proofs of these facts are left to the reader.)
Consequently, by the definition of a function, for any c in C, there must be some a in A such that
(f o g) ^-1(c) = a. We now use this as a basis to prove that (f o g) ^-1 = g ^-1 o f ^-1
.

1. (f o g) -1(c) = a implies (f o g)(a) = c	Definition of inverse function applied to (f o g)
2. (f o g)(a) = c implies f(g(a)) = c, meaning that there exists b in B such that g(a) = b and f(b) = c	Definition of composition
3. g(a) = b implies g -1(b) = a and f(b) = c implies f -1(c) = b	Definition of inverse function applied to g and f
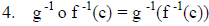	Definition of composition
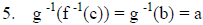	Substituting f -1(c) = b and g -1(b) = a from step 3
6. Thus,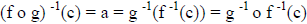	Combining steps 1, 4 and 5

Hence, we have shown that (f o g) ^-1(c) = g ^-1 o f ^-1(c) for any arbitrary c in C, where C is the
domain of (f o g) ^-1. Thus, it follows that this equality must hold generally for all elements of the
domain of (f o g) ^-1, so (f o g) ^-1 = g ^-1 o f ^-1.
QED.

Problem: Prove or disprove that

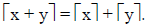
Proof: This statement is actually false. Consider the counter-example where x = ½ and y = ½.
Here, 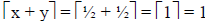, whereas

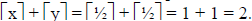
Bibliography

For additional information on functions, consult Discrete Math textbooks or Calculus
textbooks. The following are excellent references:

S. Epp, Discrete Mathematics with Applications, Belmont, CA: Wadsworth, 1990.

R. McEliece, R. Ash, C. Ash, Introduction to Discrete Mathematics, New York: Random
House, 1989.

K. Rosen, Discrete Mathematics and its Applications 6th Ed., New York: McGraw-Hill, 2007.

Historical Notes

The term "function" and the form (x, f(x)) is attributed to Leibniz who used it to refer to
several of his mathematical formulas, but the concept of a function was first presented by René
Descartes (1596-1650) in his Geometry of 1637. In this book, he presents the concept of
defining an equation in terms of one variable (i.e., as a function of...), and how to graph
equations in the Cartesian plane. The formal definition of a function (as a mapping from
domain to target) was first formulated for sets of numbers by Lejeune Dirichlet (1805-1859) in
1837.