REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA

DAVID S. WATKINS

As textbook prices head into the stratosphere, it is gratifying to observe that
some people are trying to do something about it. Robert Beezer has made his text A
First Course in Linear Algebra available to the public for free. A MathML hypertext
version is on the web at , you can download a pdf version, or
you can buy an inexpensive paper copy through the print-on-demand service lulu.com.
The online and pdf versions contain links back to all theorems, definitions, etc., as
they are used.

This book is a work in progress. There are three parts: Core, Topics, and Applications,
but only the Core part resembles a finished book. The other two are just
beginning to take form. The author envisions adding more and more to the book over
time, and he encourages all of us to help out by making contributions. To this end he
has made the TEX source code available. Users of the book are free to modify it and
share their modifications with others, subject to the terms of the GNU Free Document
License. As the author notes in the preface, “[This book] will never go ‘out of print’
nor will there ever be trivial updates designed to frustrate the used book market.”

So what is the book like? First of all, all chapters, sections, theorems, and other
items are given acronyms instead of numbers. Some examples: The chapter on vector
spaces is Chapter VS. A theorem that says that linear transformations take zero to
zero is called Theorem LTTZZ. The section on injective linear transformations is
Section ILT. This practice has the advantage that Theorem LTTZZ will always have
that name, even as the book changes shape over time. The disadvantage is that the
text is cluttered with acronyms, most of which will have no immediate meaning for
the reader.

The focus of the book is theoretical. Quoting again from the preface: “This
textbook is designed to teach the university mathematics student the basics of the
subject of linear algebra and the techniques of formal mathematics.” Thus the book
is meant for mathematics majors, and proofs and proof techniques are emphasized.
The tone of the book is mostly formal; equations are preferred over words. Most
of the proofs contain long chains of equalities like this one taken from the proof of
Theorem OSIS (one side is sufficient), which shows that a right inverse is also a left
inverse:

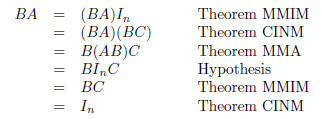
In the electronic versions, the cited theorems have links back to their statements. In
the paper version, page numbers are given.

This is a text for an algebra course. As the author states in the very first section,
“. . .we will maintain an algebraic approach to the subject, with the geometry being
secondary. . . . here and now we are laying our bias bare.” Indeed, the book is entirely
algebraic; geometry is nowhere to be found.

The book begins concretely. There is a chapter on solving linear systems using
row-echelon form. This is followed by a chapter on vectors in Cⁿ that introduces
concepts such as linear combinations, linear independence, spanning sets, and orthogonality.
Then a chapter on matrices introduces matrix operations, the matrix inverse,
null space, row space, column space, and the like. The relationships between these
concepts and the solution of linear systems are laid out. After this the book takes an
abstract turn, with chapters on vector spaces and linear transformations. Sandwiched
between these are chapters on determinants and eigenvalues of matrices. This ordering
strikes me as odd, but perhaps the order is not so important. The final chapter of
the Core part of the book is on representations of linear transformations by matrices,
culminating in the Jordan canonical form.

In my paper copy of the book, the Topics and Applications parts are empty. On
the web there are, as of this writing, a couple of sections in Applications and ten
or so in Topics. The author’s intent is that the Topics part will include topics that
the author deems not to be part of the core but that some instructors might like to
include in their courses. For example, the fact that Gaussian elimination yields an
LU decomposition of a matrix is included in Topics and not mentioned in the Core.

This choice reminds us once again of the bias of the book. This is definitely a
“pure math” treatment of linear algebra. It is assumed that all arithmetic can be done
exactly. Nowhere is it mentioned that the principal algorithms presented in the Core
break down when executed in floating-point arithmetic on a computer or calculator.
(For example, row reduction cannot determine reliably whether a square matrix is
singular or not.) Condition numbers are not mentioned, nor are the superior numerical
properties of unitary transformations. The Gram-Schmidt process is introduced in the
core, but the QR decomposition is not mentioned at all. (Hopefully it will at least be
added as a topic later.) The singular value decomposition is included as a mere topic.
We are told that it is useful, but no specific uses (e.g. reliable rank determination)
are given. Of course, all of this can be changed in the future.

Here’s one other thing I would change: The index is way too long for a single web
page. It ought to be split over many pages, perhaps 26 or so.

The preference for symbols over words sometimes has bad consequences. For
example, at the beginning of Chapter D (determinants) a square matrix 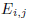is defined
as follows:

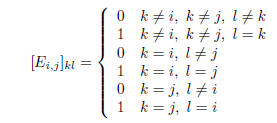
Got that? Here’s what I would have preferred: “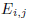 is the matrix obtained by
interchanging the ith and jth rows of the identity matrix.”

I was amused by Example CVS (crazy vector space). This is the set of all ordered
pairs of complex numbers with the operations
(x₁, x₂) + (y₁, y₂) = (x₁ + y₁ + 1, x₂ + y₂ + 1)
α(x₁, x₂) = ( αx₁ + α − 1, αx₂ + α − 1).

This really is a vector space! (What is the “zero” element?) It is a wonderful example
in the spirit of abstract algebra, but there is no way I would show it to my sophomores.
I want to develop their intuition, not crush it.

Would I use this book in my course? For me the total omission of geometry
disqualifies it immediately. A first course in linear algebra ought to contain lots of
geometry and pictures (along with the algebra) to help those sophomores develop
some insight. Moreover, at my institution the first linear algebra course is populated
mainly by engineering and science majors. They need to get the basics; they do not
need an introduction to formal mathematics. That is left for other courses, including
the second linear algebra course, which is mainly for mathematics majors. Beezer’s
book would surely be a useful supplemental resource for that course.

Clearly Beezer and I have some philosophical differences about what ought to be
in a first course in linear algebra. Nevertheless I commend him for undertaking this
project. Instructors who wish to teach a pure linear algebra course that emphasizes
rigor and formal mathematics will be able to make good use of this material and feel
secure in the knowledge that the book is not going to go out of print. Finally, the
price is right.