Integration Review Solutions

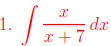
Divide x by x + 7 using long division. The quotient is 1 and the remainder -7.

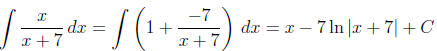
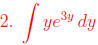
Use integration by parts: .

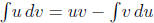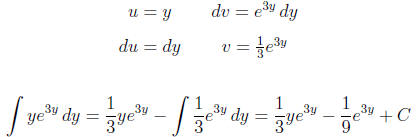
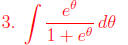
Use a u-substitution:

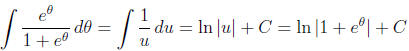
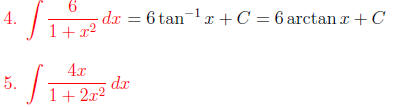
Use a u-substitution:

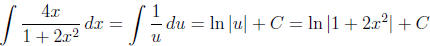
Use integration by parts: .
 

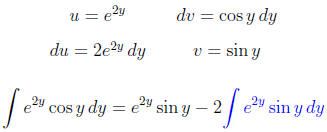
Now use integration by parts again for

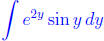
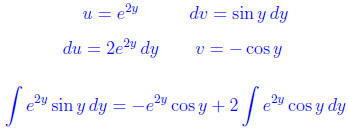
Put everything together:

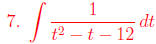
Use partial fractions.

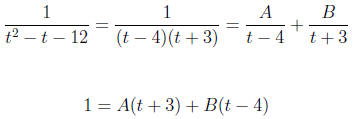
Plug in t = -3 to see that 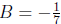. Plug in t = 4 to see that .

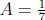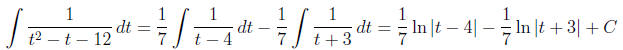
Divide t² + 2 by t + 2 using long division. The quotient is t - 2 and the remainder is 6.

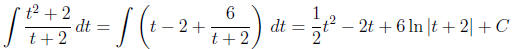
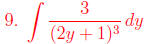
Use a u-substitution. u = 2y + 1 du = 2 dy

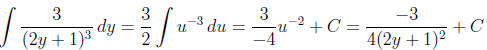
Use integration by parts multiple times, or use the D/I chart. In the first integration
by parts iteration, u = t³ and dv = e^t dt. Therefore, put t³ in the D column and put e^t in
the I column. The letter D stands for derivative and I for integral. Fill in the columns
accordingly until you get to a 0.

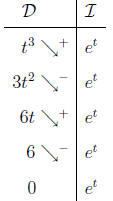
Draw diagonal arrows and label with alternating positive and negative signs. Multiply
along the diagonals, and add or subtract the resulting terms depending on the sign of the
arrow. Don't forget to add C.

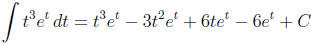
Use integration by parts: .

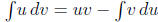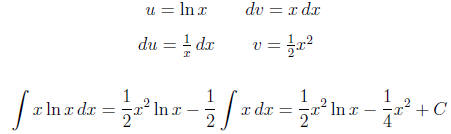
Use a trig. substitution:

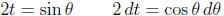
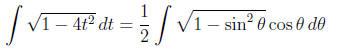
If we are careful, we see that this integral equals 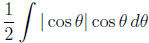. Let's assume for now
that cosθ > 0. Is this assumption valid? Think about the range of θ in the substitution.

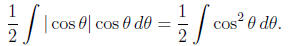
Use trig. identities to simplify.

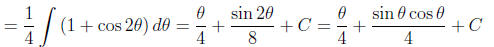
From our substitution 2t = sinθ , we deduce:

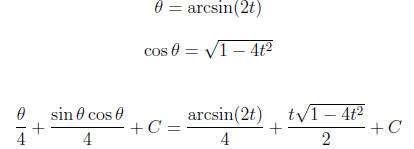
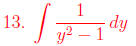
Use partial fractions.

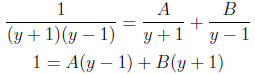
Substitute y = 1 to see that 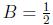and y = -1 to see that .

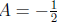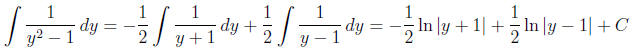
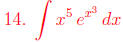
Do a z-substitution, then do integration by parts. .
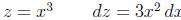